题目内容
17.已知a,b,c满足$\sqrt{b-5}$+|a-$\sqrt{8}$|+${(c-\sqrt{11})}^{2}$=0,求a,b,c的值.分析 根据非负数的性质列方程求解即可.
解答 解:∵$\sqrt{b-5}$≥0,|a-$\sqrt{8}$|≥0,${(c-\sqrt{11})}^{2}$≥0且$\sqrt{b-5}$+|a-$\sqrt{8}$|+${(c-\sqrt{11})}^{2}$=0,
∴$\sqrt{b-5}$=0,|a-$\sqrt{8}$|=0,${(c-\sqrt{11})}^{2}$=0,
∴b-5=0,a-$\sqrt{8}$=0,c-$\sqrt{11}$0,
解得a=$\sqrt{8}$=2$\sqrt{2}$,b=5,c=$\sqrt{11}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
12.A城有肥料200t,B城有肥料300t.现要把这些肥料全部运往C,D两乡,从A城往C,D两乡运肥料的费用分别为20元/t和25元/t;从B城往C,D两乡运肥料的费用分别为15元/t和24圆/t.现C乡需要肥料240t,D乡需要肥料260t.设从A城调往C乡肥料xt.
(1)根据题意,填写下表:
(2)设调运肥料的总运费y(单位:元)是x的函数,求y与x的函数解析式;
(3)请根据(2)给出完成调运任务总费用最少的调运方案,并说明理由.
(1)根据题意,填写下表:
| 调入地 水量/万吨 调出地 | C | D |
| A | x | 200-x |
| B | 240-x | 60+x |
| 总计 | 240 | 260 |
(3)请根据(2)给出完成调运任务总费用最少的调运方案,并说明理由.

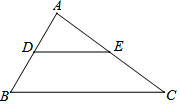 如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°;
如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°;