题目内容
2. 如图,在五边形ABCDE中,AE∥BC,∠D=∠E=∠C,求∠D的度数.
如图,在五边形ABCDE中,AE∥BC,∠D=∠E=∠C,求∠D的度数.
分析 首先利用多边形内角和公式计算出五边形ABCDE的内角和,再根据平行线的性质可得∠A+∠B=180°,进而可得∠E+∠D+∠C的度数,进而可得答案.
解答 解:五边形ABCDE的内角和为:180°×(5-2)=540°,
∵AE∥BC,
∴∠A+∠B=180°,
∴∠E+∠D+∠C=540°-180°=360°,
∵∠D=∠E=∠C,
∴∠D=360°÷3=120°.
点评 此题主要考查了多边形内角和,以及平行线的性质,关键是掌握多边形内角和公式:(n-2)•180° (n≥3)且n为整数).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.将两块长为am,宽为bm的长方形红布,加工成一个长为cm,宽为dm的长方形,有人就a,b,c,d的关系写出如下四个等式,不过他写错了一个,写错的那个是( )
| A. | $\frac{2a}{c}=\frac{d}{b}$ | B. | $\frac{a}{c}=\frac{d}{2b}$ | C. | $\frac{2a}{d}=\frac{c}{b}$ | D. | $\frac{a}{2c}=\frac{d}{b}$ |
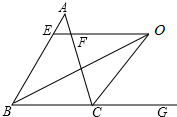 如图,在△ABC中,∠ABC的平分线与△ABC的外角平分线交于点O,过O作BC的平行线交AB于E,交AC于F.
如图,在△ABC中,∠ABC的平分线与△ABC的外角平分线交于点O,过O作BC的平行线交AB于E,交AC于F.