题目内容
10.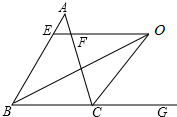 如图,在△ABC中,∠ABC的平分线与△ABC的外角平分线交于点O,过O作BC的平行线交AB于E,交AC于F.
如图,在△ABC中,∠ABC的平分线与△ABC的外角平分线交于点O,过O作BC的平行线交AB于E,交AC于F.(1)图中共有几个等腰三角形,请选择其中一个加以证明;
(2)请问线段EF与BE、CF之间存在什么数量关系.试说明理由.
分析 (1)根据角平分线的定义以及平行线的性质进行角之间的等量代换,根据等边对等角,发现两个等腰三角形:△BOE和△COF,即可得出所求的结论;
(2)根据∠ABC和∠ACG的平分线相交于点O,过点O作BC的平行线交AB于点E,可证∠EOB=∠EBO,可得BE=EO,OF=FC,于是得到结论.
解答 (1)答:图中共有△BOE和△COF2个等腰三角形;
证明:∵BO平分∠ABC,
∴∠ABO=∠OBC.
又∵EO∥BC,
∴∠EOB=∠OBC,
∴∠ABO=∠EOB,
∴BE=EO,
∴△BOE是等腰三角形.
(2)解:EF=BE-CF.
理由:∵BO平分∠ABC,
∴∠ABO=∠OBC.
又∵EO∥BC,
∴∠EOB=∠OBC,
∴∠ABO=∠EOB,
∴BE=EO,
同理可证:CF=FO,
∵EF=EO-FO,
∴EF=BE-CF.
点评 此题主要考查等腰三角形的判定与性质和平行线的性质,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 试用含x的多项式表示如图所示阴影部分的面积.
试用含x的多项式表示如图所示阴影部分的面积. 如图,在五边形ABCDE中,AE∥BC,∠D=∠E=∠C,求∠D的度数.
如图,在五边形ABCDE中,AE∥BC,∠D=∠E=∠C,求∠D的度数.