题目内容
3.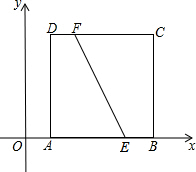 如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).
如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).
分析 根据题意得出DF=BE=1,EF的中点O是正方形的对称中心,取AG=AM=DP=1,作直线GO、MO、PO分别交CD、BC于H、N、Q,GH=MN=PQ=EF,得出AD=4,AP=3,即可得出结果.
解答 解:∵正方形ABCD是中心对称图形,DF=BE=1,
∴EF的中点O是正方形的对称中心,
∴取AG=AM=DP=1,作直线GO、MO、PO分别交CD、BC于H、N、Q,
则GH=MN=PQ=EF,如图所示:
∵AD=AB=5-1=4,
∴AP=3,
∴G(2,0),M(1,1),P(1,3);
故答案为:(1,1)、(1,3)、(2,0)
点评 本题考查了正方形的性质、坐标与图形性质以及中心对称的性质;熟练掌握正方形的性质是解决问题的关键.

练习册系列答案
相关题目
18.有下面几个样本用以统计某路口在学校放学时段的车流量情况.其中你认为合适的是( )
| A. | 抽取两天作为一个样本 | |
| B. | 选取每周星期日为样本 | |
| C. | 春、夏、秋、冬每个季节各选两周作为样本 | |
| D. | 以全年每一天为样本 |
15.下列几对数中,相等的是( )
| A. | -3和-(-3) | B. | -3和|-3| | C. | 23和3×2 | D. | -23和(-2)3 |
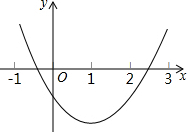 如图是某二次函数的图象,将其向右平移两个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有( )
如图是某二次函数的图象,将其向右平移两个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有( )