题目内容
1. 如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔40海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.问B处距离灯塔P有多远?(结果精确到0.1海里)
如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔40海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.问B处距离灯塔P有多远?(结果精确到0.1海里)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
分析 作PH⊥AB于H,根据正弦的定义求出PH,根据正弦的定义求出PB即可.
解答 解: 作PH⊥AB于H,
作PH⊥AB于H,
在Rt△AHP中,sin∠PAH=$\frac{PH}{PA}$,
∴PH=PA•sin∠PAH=20$\sqrt{3}$,
在Rt△BPH中,sin∠B=$\frac{PH}{PB}$
∴PB=$\frac{20\sqrt{3}}{\frac{\sqrt{2}}{2}}$=20$\sqrt{6}$≈49.0,
答:B处距离灯塔P约为49.0海里.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,已知线段AC与BC交于点C,M,N分别为线段AC与BC上的点,CN=2AM,若AC=6.
如图,已知线段AC与BC交于点C,M,N分别为线段AC与BC上的点,CN=2AM,若AC=6.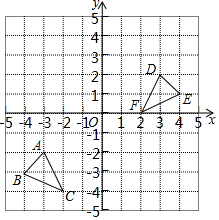 如图,方格纸中的每个小格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,方格纸中的每个小格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答下列问题: 已知:如图,点E,C在线段BF上,AC=DF,AC∥DF,BE=CF.求证:AB∥DE.
已知:如图,点E,C在线段BF上,AC=DF,AC∥DF,BE=CF.求证:AB∥DE. 如图,一副三角板的两个直角顶点重合在一起.
如图,一副三角板的两个直角顶点重合在一起.