题目内容
4.已知点A(2,1),则绕原点O逆时针旋转180°后对应点的坐标是(-2,-1).分析 根据点绕原点旋转180°,可得两点关于原点对称,根据关于原点对称的横坐标互为相反数,关于原点对称的纵坐标互为相反数,可得答案.
解答 解:由点A(2,1),则绕原点O逆时针旋转180°后对应点的坐标,得
对应点与A点关于原点对称,
对应点的坐标是(-2,-1).
故答案为:(-2,-1).
点评 本题考查了坐标与图形变化-旋转,利用点绕原点旋转180°得出两点关于原点对称是解题关键,注意关于原点对称的横坐标互为相反数,关于原点对称的纵坐标互为相反数.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
9.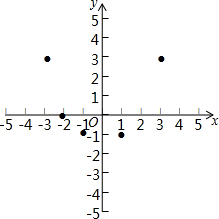 有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
小峰根据学习函数的经验,对函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质进行了探究.
下面是小峰的探究过程,请补充完整:
(1)函数y=x2-2$\sqrt{{x}^{2}}$的自变量的取值范围是任意实数;
(2)下表是y与x的几组对应值.
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,-1),结合函数的图象,写出该函数的其它性质(一条即可):对称轴是y轴.
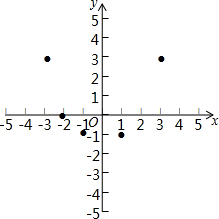 有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.小峰根据学习函数的经验,对函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质进行了探究.
下面是小峰的探究过程,请补充完整:
(1)函数y=x2-2$\sqrt{{x}^{2}}$的自变量的取值范围是任意实数;
(2)下表是y与x的几组对应值.
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | n | 3 | 0 | -1 | 0 | -1 | 0 | 3 | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,-1),结合函数的图象,写出该函数的其它性质(一条即可):对称轴是y轴.
6.下列方程组中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{3x-2y=0}\\{4x-1=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{x}^{2}-2x=y+{x}^{2}}\\{x+y=8}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x-y=6}\\{x-z=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=6}\\{2x=y}\end{array}\right.$ |
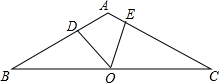 如图,△ABC中,AB=AC,∠BAC=120°,O是BC的中点,D在AB上,E在AC上,若∠DOE=60°.求证:AD+AE=$\frac{1}{2}$AB.
如图,△ABC中,AB=AC,∠BAC=120°,O是BC的中点,D在AB上,E在AC上,若∠DOE=60°.求证:AD+AE=$\frac{1}{2}$AB.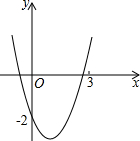 如图,已知抛物线y=x2+bx+c经过点(0,-2),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你所确定的b的值为-$\frac{7}{3}$<b<1.
如图,已知抛物线y=x2+bx+c经过点(0,-2),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你所确定的b的值为-$\frac{7}{3}$<b<1. 已知抛物线y=ax2-2ax+a-4与x轴分别交于A,B,与y轴交于C点,顶点为P.
已知抛物线y=ax2-2ax+a-4与x轴分别交于A,B,与y轴交于C点,顶点为P.