题目内容
14.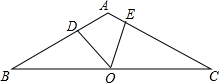 如图,△ABC中,AB=AC,∠BAC=120°,O是BC的中点,D在AB上,E在AC上,若∠DOE=60°.求证:AD+AE=$\frac{1}{2}$AB.
如图,△ABC中,AB=AC,∠BAC=120°,O是BC的中点,D在AB上,E在AC上,若∠DOE=60°.求证:AD+AE=$\frac{1}{2}$AB.
分析 取AB的中点M,连接OM,AO,根据等腰三角形的性质得出∠BAO=∠CAO=60°,AO⊥BC,根据直角三角形斜边上中线性质得出OM=AM=BM,求出△AOM是等边三角形,推出AO=OM,∠AOM=60°,∠DMO=∠OAE=60°,求出∠AOE=∠MOD,根据ASA推出△AOE≌△MOD,根据全等得出AE=DM,即可得出答案.
解答 证明:如图: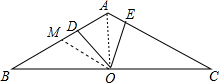
取AB的中点M,连接OM,AO,
∵在△ABC中,AB=AC,∠BAC=120°,
∴∠BAO=∠CAO=60°,AO⊥BC,
∴∠AOB=90°,
∴OM=AM=BM,
∵∠OAM=60°,
∴△AOM是等边三角形,
∴AO=OM,∠AOM=60°,∠DMO=∠OAE=60°,
∵∠DOE=60°,
∴∠AOM=∠DOE,
∴都减去∠AOD得:∠AOE=∠MOD,
在△AOE和△MOD中,
$\left\{\begin{array}{l}{∠AOE=∠MOD}\\{AO=MO}\\{∠EAO=∠DMO}\end{array}\right.$,
∴△AOE≌△MOD(ASA),
∴AE=DM,
∴AE+AD=AM,
∵AM=BM=$\frac{1}{2}$AB,
∴AD+AE=$\frac{1}{2}$AB.
点评 本题考查了全等三角形的性质和判定,等腰三角形的性质,等边三角形的性质和判定,直角三角形斜边上中线性质的应用,能灵活运用定理进行推理是解此题的关键,注意:全等三角形的对应边相等.

练习册系列答案
相关题目
4.下列结论不正确的是( )
| A. | 若a>0,b<0,且a>|b|,则a+b<0 | B. | 若a<0,b>0,且|a|>b,则a+b<0 | ||
| C. | 若a>0,b>0,则a+b>0 | D. | 若a<0,b<0,则a+b<0 |
2.某商店在一次买卖中,同时卖出两种货物,每种货物的售价均为960元.若按成本计算,一种货物盈利20%,另一种亏本20%,则这次交易商店( )
| A. | 赚160元 | B. | 赔80元 | C. | 赔240元 | D. | 赚400元 |
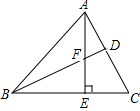 如图,AE是△ABC的高,D为AC上一点,AE交BD于点F,且FE=CE,BF=AC.求证:BD⊥AC.
如图,AE是△ABC的高,D为AC上一点,AE交BD于点F,且FE=CE,BF=AC.求证:BD⊥AC.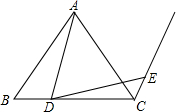 如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,
如图,等腰△ABC,AB=AC,D是BC边上一点,射线CE∥AB,且AD=DE,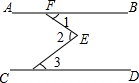 如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°.
如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°.