题目内容
13.方程3x2-2$\sqrt{6}$x+2=0的根的情况是( )| A. | 无实根 | B. | 有两个等根 | C. | 有两个不等根 | D. | 有分数根 |
分析 先求一元二次方程的判别式,由△与0的大小关系来判断方程根的情况.
解答 解:∵a=3,b=-2$\sqrt{6}$,c=2,
∴△=b2-4ac=24-24=0,
∴一元二次方程有两个相等的实数根.
故选B.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
18.已知x,y满足$\left\{\begin{array}{l}{2x-3y=1①}\\{3x-2y=5②}\end{array}\right.$,如果①×a+②×b可整体得到x+11y的值,那么a,b的值可以是( )
| A. | a=2,b=-1 | B. | a=-4,b=3 | C. | a=1,b=-7 | D. | a=-7,b=5 |
5.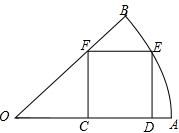 如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )
如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )
 如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )
如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )| A. | π:8 | B. | 5π:8 | C. | $\sqrt{3}$π:4 | D. | $\sqrt{5}$π:4 |
2.下列运算正确的是( )
| A. | a2•a2=a4 | B. | (a-b)2=a2-b2 | C. | 2+$\sqrt{2}$=2$\sqrt{2}$ | D. | (-a3)2=-a6 |
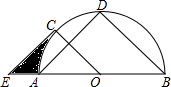 如图所示,AB为半圆O的直径,点D是半圆弧的中点,半径OC∥BD,过点C作AD的平行线交BA延长线于点E.
如图所示,AB为半圆O的直径,点D是半圆弧的中点,半径OC∥BD,过点C作AD的平行线交BA延长线于点E. 已知:⊙O的半径为5,PO=3
已知:⊙O的半径为5,PO=3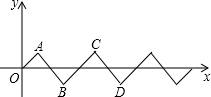 如图,在平面直角坐标系中,将斜边长为2个等腰直角三角形按如图所示的位置摆放,得到一条折线O-A-B-C-D…,点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动,2016秒时,点P的坐标是(2016,0).
如图,在平面直角坐标系中,将斜边长为2个等腰直角三角形按如图所示的位置摆放,得到一条折线O-A-B-C-D…,点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动,2016秒时,点P的坐标是(2016,0).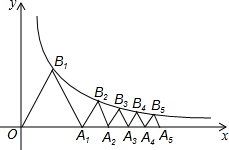 如图,点A1、A2、A3、A4、A5、…、A2015在x轴的正半轴上,点B1、B2、B3、B4、B5、…、B2015在双曲线y=$\frac{\sqrt{3}}{x}$上,若△A1B1O、△A2B2A1、△A3B3A2、△A4B4A3、△A5B5A4、…、△A2015B2015A2014均为等边三角形,求△A2015B2015A2014的边长.
如图,点A1、A2、A3、A4、A5、…、A2015在x轴的正半轴上,点B1、B2、B3、B4、B5、…、B2015在双曲线y=$\frac{\sqrt{3}}{x}$上,若△A1B1O、△A2B2A1、△A3B3A2、△A4B4A3、△A5B5A4、…、△A2015B2015A2014均为等边三角形,求△A2015B2015A2014的边长.