题目内容
10.阅读下列解答过程:已知:x≠0,且满足x2-3x=1.求:${x^2}+\frac{1}{x^2}$的值.
解:∵x2-3x=1,∴x2-3x-1=0
∴$x-3-\frac{1}{x}=0$,即$x-\frac{1}{x}=3$.
∴${x^2}+\frac{1}{x^2}$=${({x-\frac{1}{x}})^2}+2$=32+2=11.
请通过阅读以上内容,解答下列问题:
已知a≠0,且满足(2a+1)(1-2a)-(3-2a)2+9a2=14a-7,
求:(1)${a^2}+\frac{1}{a^2}$的值;(2)$\frac{a^2}{{5{a^4}+{a^2}+5}}$的值.
分析 (1)根据题意可得$a-\frac{1}{a}=2$,再利用完全平方公式计算即可;
(2)根据倒数的定义和完全平方公式计算即可.
解答 解:(1)(2a+1)(1-2a)-(3-2a)2+9a2=14a-71-4a2-(9-12a+4a2)+9a2-14a+7=0,
整理得:a2-2a-1=0
∴$a-\frac{1}{a}=2$,
∴${a^2}+\frac{1}{a^2}={({a-\frac{1}{a}})^2}+2=4+2=6$;
(2)解:$\frac{a^2}{{5{a^4}+{a^2}+5}}$的倒数为$\frac{{5{a^4}+{a^2}+5}}{a^2}$,
∵$\frac{{5{a^4}+{a^2}+5}}{a^2}=5{a^2}+\frac{5}{a^2}+1=5({{a^2}+\frac{1}{a^2}})+1=5×6+1=31$,
∴$\frac{a^2}{{5{a^4}+{a^2}+5}}=\frac{1}{31}$.
点评 此题考查完全平方公式,关键是根据完全平方公式进行变形解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.二次函数y=(m-2)x2+m2+2m-8中,当x=0时,y=0,那么当x=2时,y的值应为( )
| A. | 2 | B. | -24 | C. | 24 | D. | -2 |
15.从长度分别为2cm、3cm、4cm、5cm的四条线段中任选三条线段能组成三角形的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
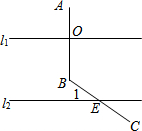 如图,l1∥l2,AB⊥l1,垂足为O,BC交l2于点E,若∠ABC=140°,求∠1的度数.
如图,l1∥l2,AB⊥l1,垂足为O,BC交l2于点E,若∠ABC=140°,求∠1的度数.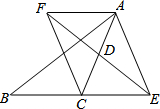 已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE,CF.试猜想线段AF与线段CE有何关系,并说明原因.
已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE,CF.试猜想线段AF与线段CE有何关系,并说明原因.