题目内容
14. 已知P是平行四边形ABCD内一点,若S△ABP:SABCD=2:5,则S△CPD:SABCD=1:10.
已知P是平行四边形ABCD内一点,若S△ABP:SABCD=2:5,则S△CPD:SABCD=1:10.
分析 可由三角形的面积入手,建立平衡,进而即可求解.
解答 解:由题意可得,S△ABP+S△CDP=S△ADP+S△BCP=$\frac{1}{2}$SABCD
又S△ABP:SABCD=2:5,
∴可得S△CPD:SABCD=1:10,
故答案为1:10.
点评 本题主要考查平行四边形的性质及三角形的面积问题,应熟练掌握平行四边形的性质,能够求解一些简单的计算问题.

练习册系列答案
相关题目
9.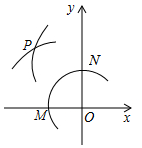 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )| A. | a=b | B. | 2a-b=1 | C. | 2a+b=-1 | D. | 2a+b=1 |
6. 图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
 图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )| A. | 体育场离张强家2.5千米 | |
| B. | 张强在体育场锻炼了15分钟 | |
| C. | 体育场离早餐店4千米 | |
| D. | 张强从早餐店回家的平均速度是$\frac{18}{7}$千米/小时 |
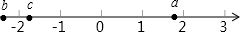 实数a、b、c在数轴上的对应点如图所示,其中|a|=|c|,化简|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c.
实数a、b、c在数轴上的对应点如图所示,其中|a|=|c|,化简|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c.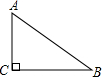 如图所示,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使点C为正方的一个顶点,其余三个顶点分别在AB、BC、AC上.
如图所示,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使点C为正方的一个顶点,其余三个顶点分别在AB、BC、AC上. 如图,线段DE由线段AB平移而得,AB=4,EC=7-CD,则△DCE的周长为11 cm.
如图,线段DE由线段AB平移而得,AB=4,EC=7-CD,则△DCE的周长为11 cm.