题目内容
20.三名运动员参加定点投篮比赛,原定出场顺序是:甲第一个出场,乙第二个出场,丙第三个出场.由于某种原因,要求这三名运动员用抽签方式重新确定出场顺序,则抽签后每个运动员的出场顺序都发生变化的概率为$\frac{1}{3}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与抽签后每个运动员的出场顺序都发生变化的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有6种等可能的结果,抽签后每个运动员的出场顺序都发生变化有2种情况,
∴抽签后每个运动员的出场顺序都发生变化的概率=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
15.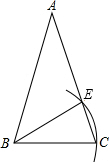 如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
 如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )| A. | AE=EC | B. | AE=BE | C. | ∠EBC=∠BAC | D. | ∠EBC=∠ABE |
5. 已知直线a∥b,一块含30°角的直角三角尺如图放置.若∠1=25°,则∠2等于( )
已知直线a∥b,一块含30°角的直角三角尺如图放置.若∠1=25°,则∠2等于( )
 已知直线a∥b,一块含30°角的直角三角尺如图放置.若∠1=25°,则∠2等于( )
已知直线a∥b,一块含30°角的直角三角尺如图放置.若∠1=25°,则∠2等于( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
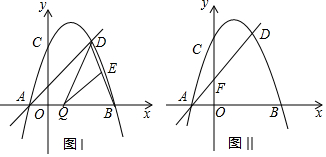
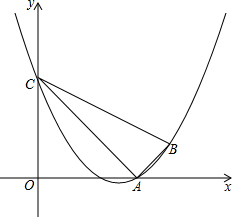 如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y轴交于点C,连接AB、AC、BC.
如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y轴交于点C,连接AB、AC、BC.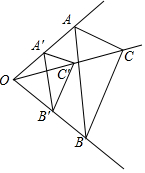 如图,若△A'B'C'与△ABC位似,相似比为k.
如图,若△A'B'C'与△ABC位似,相似比为k.