题目内容
3.在一个不透明的袋子中有6个白球,k个红球,这些球除颜色外其他都相同,经过试验从中任取一个球恰好为红球的概率为$\frac{1}{4}$,则k的值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据红球的概率公式列出关于k的解析式,再求出k的值即可.
解答 解:因为袋子中有6个白球,k个红球,共k+2个,经过实验从中任取一个球恰好为红球的概率为0.25,即有$\frac{k}{k+6}$=$\frac{1}{4}$,解得k=2.
故选:A.
点评 本题考查的是概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
12.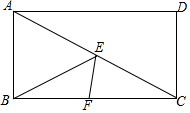 如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )
如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )
 如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )
如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )| A. | $\frac{16}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
13.下列各式计算正确的是( )
| A. | 2$\sqrt{3}$-$\sqrt{3}$=2 | B. | 2$\sqrt{3}$+$\sqrt{2}$=2$\sqrt{5}$ | C. | 4$\sqrt{2}$×2$\sqrt{2}$=8$\sqrt{2}$ | D. | 4$\sqrt{6}$÷2$\sqrt{2}$=2$\sqrt{3}$ |
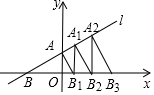 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}-\sqrt{3}$.
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}-\sqrt{3}$.
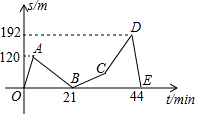 爸爸和小芳驾车去郊外登山,欣赏美丽的达子香(兴安杜鹃),到了山下,爸爸让小芳先出发6min,然后他再追赶,待爸爸出发24min时,妈妈来电话,有急事,要求立即回去.于是爸爸和小芳马上按原路下山返回(中间接电话所用时间不计),二人返回山下的时间相差4min,假设小芳和爸爸各自上、下山的速度是均匀的,登山过程中小芳和爸爸之间的距离s(单位:m)关于小芳出发时间t(单位:min)的函数图象如图,请结合图象信息解答下列问题:
爸爸和小芳驾车去郊外登山,欣赏美丽的达子香(兴安杜鹃),到了山下,爸爸让小芳先出发6min,然后他再追赶,待爸爸出发24min时,妈妈来电话,有急事,要求立即回去.于是爸爸和小芳马上按原路下山返回(中间接电话所用时间不计),二人返回山下的时间相差4min,假设小芳和爸爸各自上、下山的速度是均匀的,登山过程中小芳和爸爸之间的距离s(单位:m)关于小芳出发时间t(单位:min)的函数图象如图,请结合图象信息解答下列问题: