题目内容
2．一个凸多边形的每个内角都是140°，这个多边形共有多少条对角线？分析 先求出多边形的外角度数，然后即可求出边数，再利用公式$\frac{1}{2}$n（n-3）代入数据计算即可．
解答 解：∵多边形的每个内角都等于140°，
∴多边形的每个外角都等于180°-140°=40°，
∴边数n=360°÷40°=9，
∴对角线条数=$\frac{1}{2}$×9×（9-3）=27．
故这个多边形共有27条对角线．
点评 本题主要考查了多边形的外角与对角线的性质，求出边数是解题的关键，另外熟记从多边形的对角线的条数公式也很重要．
练习册系列答案
相关题目
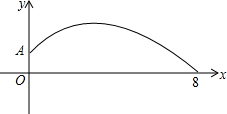某学校在一次投掷铅球时，刚出手时铅球离地面$\frac{5}{3}$m，铅球运行的水平距离为4m时，达到最高，高度为3m，如图所示：
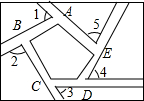清晨，小强沿着一个五边形广场周围的小路，按逆时针方向跑步．
如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数．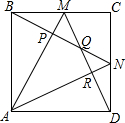
如图，M、N是单位正方形ABCD边BC、CD的中点，连接AM、DM、AN、BN，则这些线段所围成的四边形APQR的面积是$\frac{4}{15}$．