题目内容
8.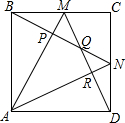 如图,M、N是单位正方形ABCD边BC、CD的中点,连接AM、DM、AN、BN,则这些线段所围成的四边形APQR的面积是$\frac{4}{15}$.
如图,M、N是单位正方形ABCD边BC、CD的中点,连接AM、DM、AN、BN,则这些线段所围成的四边形APQR的面积是$\frac{4}{15}$.
分析 连接AC、PR、MN,如图所示.根据轴对称的性质可得:点Q在AC上,PR∥MN,AC⊥PR.由AC⊥PR可得S四边形APQR=$\frac{1}{2}$AQ•PR,只需证明△APR∽△AMN及△ABQ∽△CNQ,然后运用相似的三角形的性质求出PR及AQ,即可解决问题.
解答  解:连接AC、PR、MN,如图所示.
解:连接AC、PR、MN,如图所示.
根据轴对称的性质可得:点Q在AC上,PR∥MN,AC⊥PR.
由tan∠CBN=$\frac{1}{2}$=tan∠BAM可得∠CBN=∠BAM,由此可得∠APB=90°.
由cos∠BAM=$\frac{AP}{AB}$=$\frac{AB}{AM}$,AM=$\sqrt{1+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$,AB=1可得AP=$\frac{2\sqrt{5}}{5}$.
由PR∥MN可得△APR∽△AMN,从而可得$\frac{PR}{MN}$=$\frac{AP}{AM}$=$\frac{4}{5}$.
由MN=$\sqrt{\frac{1}{4}+\frac{1}{4}}$=$\frac{\sqrt{2}}{2}$可得PR=$\frac{2\sqrt{2}}{5}$.
由AB∥CD可得△ABQ∽△CNQ,从而可得$\frac{AQ}{CQ}$=$\frac{AB}{CN}$=2,
即可得到AQ=$\frac{2}{3}$AC=$\frac{2\sqrt{2}}{3}$.
由AC⊥PR可得S四边形APQR=$\frac{1}{2}$AQ•PR=$\frac{1}{2}$×$\frac{2\sqrt{2}}{3}$×$\frac{2\sqrt{2}}{5}$=$\frac{4}{15}$.
故答案为$\frac{4}{15}$.
点评 本题主要考查了正方形的性质、轴对称的性质,对角线互相垂直的三角形面积公式、相似三角形的判定与性质、三角函数的定义等知识,巧妙地运用轴对称的性质是解决本题的关键.

| A. | x=0 | B. | x≠0 | C. | x≠1 | D. | x=1 |
| A. | x(x2-2) | B. | x(x-1)2 | C. | x(x-$\sqrt{2}$)(x$+\sqrt{2}$) | D. | x(x-$\sqrt{2}$)2 |
| A. | (-p2q)3=-p5q3 | B. | (12a2b3c)÷(6ab2)=2ab | ||
| C. | (x2-4x)x-1=x-4 | D. | 3m2÷(3m-1)=m-3m2 |
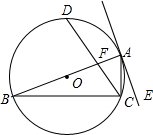 如图,AB是⊙O的直径,AE是⊙O的切线,C是⊙O上一点,CD平方∠ACB,若∠CAE=21°,则∠BFC的度数为114°.
如图,AB是⊙O的直径,AE是⊙O的切线,C是⊙O上一点,CD平方∠ACB,若∠CAE=21°,则∠BFC的度数为114°.