题目内容
如果我们定义:“到三角形的两个顶点距离相等的点,叫做此三角形的准外心.”例如,如图(1),若PC=PB,则P为△ABC的准外心.
(1)如图(1),观察并思考,△ABC的准外心有 个;
(2)如图(2),CD为等边三角形ABC的高,准外心P在高CD上,且PD=
AB,则∠APB的度数为 ;
(3)如图(3),直线y=
x+8点A,交y轴于点B,若点P是△AOB的准外心,且点P在OB上,求点P的坐标.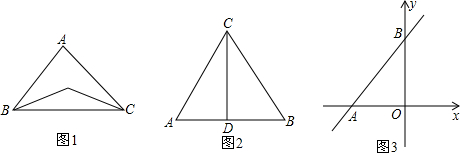
(1)如图(1),观察并思考,△ABC的准外心有
(2)如图(2),CD为等边三角形ABC的高,准外心P在高CD上,且PD=
| 1 |
| 2 |
(3)如图(3),直线y=
| 4 |
| 3 |

考点:一次函数综合题,三角形的外接圆与外心
专题:新定义
分析:(1)根据题中的新定义得到到三角形的两个顶点距离相等的点有无数个,即△ABC的准外心有无数个;
(2)根据题意得到三角形PAD与三角形PBD都为等腰直角三角形,进而确定出∠APB的度数;
(3)根据直线与y轴交于点B,确定出B的坐标,分两种情况考虑:(i)若PB=PO,即P为OB中点时,求出P坐标;(ii)若PA=PB,即P为线段AB垂直平分线与y轴交点时,求出P坐标即可.
(2)根据题意得到三角形PAD与三角形PBD都为等腰直角三角形,进而确定出∠APB的度数;
(3)根据直线与y轴交于点B,确定出B的坐标,分两种情况考虑:(i)若PB=PO,即P为OB中点时,求出P坐标;(ii)若PA=PB,即P为线段AB垂直平分线与y轴交点时,求出P坐标即可.
解答: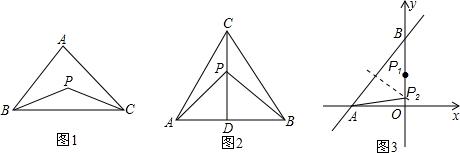 解:(1)如图(1),观察并思考,△ABC的准外心有无数个;
解:(1)如图(1),观察并思考,△ABC的准外心有无数个;
(2)∵CD为等边三角形ABC的高,
∴AD=BD=
AB,
∵PD=
AB,
∴PA=AD=BD,
∵∠PDA=∠PDB=90°,
∴△PAD与△PBD都为等腰直角三角形,
∴∠APD=∠BPD=45°,
∴∠APB=90°;
(3)对于直线y=
x+8,令x=0,得到y=8;令y=0,得到x=-6,
∴A(-6,0),B(0,8),
分两种情况考虑:
(i)当P1为线段OB中点时,点P1是△AOB的准外心,此时P1坐标为(0,4);
(ii)当P2是边AB垂直平分线与y轴交点时,点P2是△AOB的准外心,
线段AB的垂直平分线方程为y-4=-
(x+3),
令x=0,得到y=4-
=
,此时P2坐标为(0,
).
故答案为:(1)无数;(2)90°.
 解:(1)如图(1),观察并思考,△ABC的准外心有无数个;
解:(1)如图(1),观察并思考,△ABC的准外心有无数个;(2)∵CD为等边三角形ABC的高,
∴AD=BD=
| 1 |
| 2 |
∵PD=
| 1 |
| 2 |
∴PA=AD=BD,
∵∠PDA=∠PDB=90°,
∴△PAD与△PBD都为等腰直角三角形,
∴∠APD=∠BPD=45°,
∴∠APB=90°;
(3)对于直线y=
| 4 |
| 3 |
∴A(-6,0),B(0,8),
分两种情况考虑:
(i)当P1为线段OB中点时,点P1是△AOB的准外心,此时P1坐标为(0,4);
(ii)当P2是边AB垂直平分线与y轴交点时,点P2是△AOB的准外心,
线段AB的垂直平分线方程为y-4=-
| 3 |
| 4 |
令x=0,得到y=4-
| 9 |
| 4 |
| 7 |
| 4 |
| 7 |
| 4 |
故答案为:(1)无数;(2)90°.
点评:此题属于一次函数综合题,涉及的知识有:等腰直角三角形的判定与性质,一次函数与坐标轴的交点,弄清题中的新定义是解本题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
下列说法中,正确的是( )
| A、任何数的平方根都有2个 |
| B、一个正数的平方根的平方就是它本身 |
| C、只有正数才有平方根 |
| D、-3不是9的平方根 |
已知锐角A,且sinA=
,则∠A等于( )
| ||
| 2 |
| A、30° | B、45° |
| C、15° | D、60° |
 如图,表示△AOB以O为位似中心,扩大到△COD,各点坐标分别为:A(1,2)、B(3,0)、D(6,0),则点C坐标为( )
如图,表示△AOB以O为位似中心,扩大到△COD,各点坐标分别为:A(1,2)、B(3,0)、D(6,0),则点C坐标为( )| A、(2,3) |
| B、(2,4) |
| C、(3,3) |
| D、(3,4) |
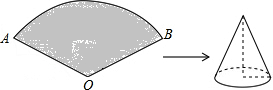 如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为
如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为 在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,3),B(2,1),C(3,2).
在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,3),B(2,1),C(3,2).