题目内容
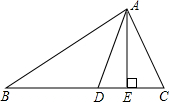如图，AE，AD分别是△ABC的高和角平分线，且∠B=40°，∠C=60°，求∠BAD和∠DAE的度数．考点：三角形的角平分线、中线和高,三角形内角和定理
专题：
分析：△ABC中已知∠B=40°，∠C=60°，根据三角形的内角和定理得到∠BAC的度数，再利用角平分线的性质可求出∠BAD，根据三角形外角的性质求出∠ADE，则∠DAE=90°-∠ADE．
解答：解：∵∠B=40°，∠C=60°，
∴∠BAC=180°-∠B-∠C=80°．
∵AD是△ABC的角平分线，
∴∠BAD=∠DAC=
∠BAC=40°，
∴∠ADE=∠B+∠BAD=80°，
∴∠DAE=90°-∠ADE=90°-80°=10°．
∴∠BAC=180°-∠B-∠C=80°．
∵AD是△ABC的角平分线，
∴∠BAD=∠DAC=
| 1 |
| 2 |
∴∠ADE=∠B+∠BAD=80°，
∴∠DAE=90°-∠ADE=90°-80°=10°．
点评：本题考查的是三角形的角平分线和高的定义，三角形内角和定理，三角形外角的性质，熟知三角形的内角和是180°是解答此题的关键．
练习册系列答案
相关题目
2013年12月15日，嫦娥三号着陆器、巡视器顺利完成互拍，把成像从远在地球38万km之外的月球传到地面，标志着我国探月工程二期取得圆满成功，将38万用科学记数法表示应为（ ）
| A、0.38×106 |
| B、0.38×105 |
| C、3.8×104 |
| D、3.8×105 |
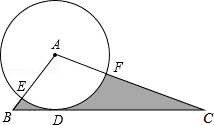如图，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，且∠EAF=80°，则图中阴影部分的面积为（ ）| A、4 | ||
B、
| ||
C、4-
| ||
D、8-
|
下列图形对称轴最多的是（ ）
| A、正方形 | B、等边三角形 |
| C、等腰三角形 | D、线段 |
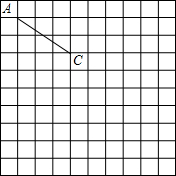如图，在正方形网格中，每个小正方形的边长为1个单位长度，已知△ABC的顶点A、C的坐标分别为（-4，4）、（-1，2），点B坐标为（-2，1）．