题目内容
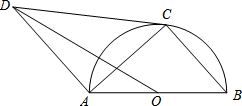 如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连结OD,AC.
如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连结OD,AC.(1)求证:∠B=∠DCA;
(2)若tanB=
| ||
| 2 |
| 6 |
考点:切线的性质
专题:
分析:(1)首先连接OC,由CD与⊙O相切,AB是⊙O的直径,易证得∠2+∠3=90°,∠1+∠B=90°,又由OA=OC,则可证得:∠B=∠DCA;
(2)由AD∥BC,AB是⊙O的直径,易证得△ABC∽△DCA,则可得
=
,又由∠B的正切值为
,可得:AC=
k,BC=2k,则AB=3k,继而表示出DC的长,然后由勾股定理,可得(
k)2+(
k)2=(3
)2,则可求得答案.
(2)由AD∥BC,AB是⊙O的直径,易证得△ABC∽△DCA,则可得
| AC |
| DC |
| BC |
| AB |
| ||
| 2 |
| 5 |
3
| ||
| 2 |
| 3 |
| 2 |
| 6 |
解答: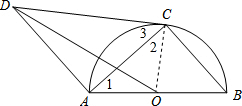 (1)证明:连结OC.
(1)证明:连结OC.
∵CD与⊙O相切,OC为半径,
∴∠2+∠3=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠1+∠B=90°,
又∵OA=OC,
∴∠1=∠2,
∴∠3=∠B,
即∠B=∠DCA.
(2)解:∵AD∥BC,AB是⊙O的直径,
∴∠DAC=∠ACB=90°,
∵∠1+∠B=90°,∠2+∠3=90°,∠1=∠2,
∴∠B=∠3,
∴△ABC∽△DCA,
∴
=
,
∵∠B的正切值为
,
设AC=
k,BC=2k,则AB=3k,
∴
=
,
∴DC=
,
在△ODC中,OD=3
,OC=
AB=
k,
∴(
k)2+(
k)2=(3
)2,
∴解得:k=2,
∴⊙O的半径长为3.
 (1)证明:连结OC.
(1)证明:连结OC.∵CD与⊙O相切,OC为半径,
∴∠2+∠3=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠1+∠B=90°,
又∵OA=OC,
∴∠1=∠2,
∴∠3=∠B,
即∠B=∠DCA.
(2)解:∵AD∥BC,AB是⊙O的直径,
∴∠DAC=∠ACB=90°,
∵∠1+∠B=90°,∠2+∠3=90°,∠1=∠2,
∴∠B=∠3,
∴△ABC∽△DCA,
∴
| AC |
| DC |
| BC |
| AB |
∵∠B的正切值为
| ||
| 2 |
设AC=
| 5 |
∴
| ||
| DC |
| 2 |
| 3 |
∴DC=
3
| ||
| 2 |
在△ODC中,OD=3
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
∴(
3
| ||
| 2 |
| 3 |
| 2 |
| 6 |
∴解得:k=2,
∴⊙O的半径长为3.
点评:此题考查了切线的性质、相似三角形的判定与性质以及勾股定理等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2013年12月15日,嫦娥三号着陆器、巡视器顺利完成互拍,把成像从远在地球38万km之外的月球传到地面,标志着我国探月工程二期取得圆满成功,将38万用科学记数法表示应为( )
| A、0.38×106 |
| B、0.38×105 |
| C、3.8×104 |
| D、3.8×105 |
下列说法正确的有( )
①没有绝对值最小的有理数;
②最大的负整数是-1;
③0是最小的整数;
④有理数分为整数和分数.
①没有绝对值最小的有理数;
②最大的负整数是-1;
③0是最小的整数;
④有理数分为整数和分数.
| A、4个 | B、3个 | C、2个 | D、1个 |
下列事件中,属于必然事件的是( )
| A、购买一张彩票,中奖 |
| B、打开电视,正在播放广告 |
| C、抛掷一枚硬币,正面向上 |
| D、通常情况下,水加热到100℃沸腾 |
在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinA是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
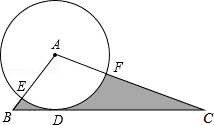 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积为( )
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积为( )| A、4 | ||
B、
| ||
C、4-
| ||
D、8-
|
 如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E.CE=1,ED=3,求AB长.
如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E.CE=1,ED=3,求AB长.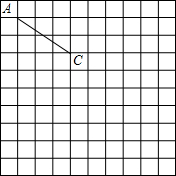 如图,在正方形网格中,每个小正方形的边长为1个单位长度,已知△ABC的顶点A、C的坐标分别为(-4,4)、(-1,2),点B坐标为(-2,1).
如图,在正方形网格中,每个小正方形的边长为1个单位长度,已知△ABC的顶点A、C的坐标分别为(-4,4)、(-1,2),点B坐标为(-2,1).