题目内容
14.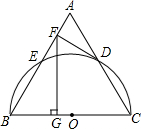 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )| A. | 4 | B. | 6 | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 连接OD,由DF为圆的切线,利用切线的性质得到OD垂直于DF,根据三角形ABC为等边三角形,利用等边三角形的性质得到三条边相等,三内角相等,都为60°,由OD=OC,得到三角形OCD为等边三角形,进而得到OD平行与AB,由O为BC的中点,得到D为AC的中点,在直角三角形ADF中,利用30°所对的直角边等于斜边的一半求出AD的长,进而求出AC的长,即为AB的长,由AB-AF求出FB的长,在直角三角形FBG中,利用30°所对的直角边等于斜边的一半求出BG的长,再利用勾股定理即可求出FG的长.
解答 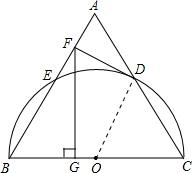 解:连接OD,
解:连接OD,
∵DF为圆O的切线,
∴OD⊥DF,
∵△ABC为等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵OD=OC,
∴△OCD为等边三角形,
∴∠CDO=∠A=60°,∠ABC=∠DOC=60°,
∴OD∥AB,
∴DF⊥AB,
在Rt△AFD中,∠ADF=30°,AF=2,
∴AD=4,即AC=8,
∴FB=AB-AF=8-2=6,
在Rt△BFG中,∠BFG=30°,
∴BG=3,
则根据勾股定理得:FG=3$\sqrt{3}$.
故选:C.
点评 此题考查了切线的性质,等边三角形的性质,含30°直角三角形的性质,勾股定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
9.已知x2-2x-5=0,则2x2-4x的值为( )
| A. | -10 | B. | 10 | C. | -2或10 | D. | 2或-10 |
19.-5的绝对值是( )
| A. | $\frac{1}{5}$ | B. | 5 | C. | -$\frac{1}{5}$ | D. | -5 |
6.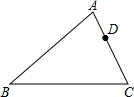 如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( )
如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( )
 如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( )
如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( )| A. | $\frac{8}{3}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | $\frac{8}{3}$或$\frac{3}{2}$ |
4.下列运算中,正确的是( )
| A. | m2×m3=m6 | B. | (m3)2=m5 | C. | m+m2=2m3 | D. | -m3÷m2=-m |
 如图,点E,F在BC上,∠DEC=∠AFB,BE=FC,AG=DG.求证:∠A=∠D.
如图,点E,F在BC上,∠DEC=∠AFB,BE=FC,AG=DG.求证:∠A=∠D.