题目内容
如图，一圆与平面直角坐标系中的x轴切于点A，与y轴交于点B（0，4），C（0，16），该圆的半径为10，则A点的坐标为考点：切线的性质,坐标与图形性质,勾股定理,垂径定理
专题：
分析：设圆的圆心是D，连接AD，作DE⊥BC于点E，连接DB，利用垂直定理求得BE的长，然后在直角三角形中利用勾股定理求得DE的长，即OA的长，则A的坐标即可求解．
解答：
解：设圆的圆心是D，连接AD，作DE⊥BC于点E，连接DB．
∵B（0，4），C（0，16），
∴BC=12，
∵DE⊥BC，
∴BE=
BC=6，
在直角△BDE中，DE=
=
=8．
则OA=DE=8．
故A的坐标是（8，0）．
解：设圆的圆心是D，连接AD，作DE⊥BC于点E，连接DB．∵B（0，4），C（0，16），
∴BC=12，
∵DE⊥BC，
∴BE=
| 1 |
| 2 |
在直角△BDE中，DE=
| BD2-BE2 |
| 102-62 |
则OA=DE=8．
故A的坐标是（8，0）．
点评：本题考查了垂径定理，注意求A的坐标就是求弦BC的弦心距，常用的方法是转化为解直角三角形．
练习册系列答案
相关题目
如图，P1、P2、P3…PK分别是抛物线y=x2上的点，其横坐标分别是1，2，3…K，记△OP1P2的面积为S1，△OP2P3的面积为S2，△OP3P4的面积为S3，则S10=
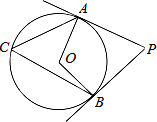如图，AP、BP分别切⊙O于点A、B，∠P=60°，点C是圆上一动点，则∠C的度数为（ ）| A、60 | B、40 |
| C、72° | D、60°或120° |