题目内容
 如图,P为⊙O的直径EF延长线上一点,PA交⊙O于B、A两点,PC交⊙O于点D、C两点,且AB=CD,求证:
如图,P为⊙O的直径EF延长线上一点,PA交⊙O于B、A两点,PC交⊙O于点D、C两点,且AB=CD,求证:(1)∠1=∠2;
(2)PB=PD.
考点:垂径定理,全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:(1)过点O分别作OE⊥AB,OH⊥CD于点E、H,再根据HL定理得出△OEP≌△OHP,根据全等三角形的性质即可得出结论;
(2)根据(1)中△OEP≌△OHP可知PE=PH,再由AB=CD可知BE=DH,故可得出结论.
(2)根据(1)中△OEP≌△OHP可知PE=PH,再由AB=CD可知BE=DH,故可得出结论.
解答: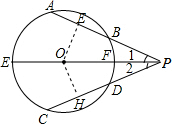 (1)证明:过点O分别作OE⊥AB,OH⊥CD于点E、H,
(1)证明:过点O分别作OE⊥AB,OH⊥CD于点E、H,
∵AB=CD,
∴OE=OH,
在Rt△OEP与Rt△OHP中,
∵
,
∴△OEP≌△OHP(HL).
∴∠1=∠2;
(2)证明:∵△OEP≌△OHP,
∴PE=PH.
∵AB=CD,OE⊥AB,OH⊥CD,
∴BE=DH,
∴PB=PD.
 (1)证明:过点O分别作OE⊥AB,OH⊥CD于点E、H,
(1)证明:过点O分别作OE⊥AB,OH⊥CD于点E、H,∵AB=CD,
∴OE=OH,
在Rt△OEP与Rt△OHP中,
∵
|
∴△OEP≌△OHP(HL).
∴∠1=∠2;
(2)证明:∵△OEP≌△OHP,
∴PE=PH.
∵AB=CD,OE⊥AB,OH⊥CD,
∴BE=DH,
∴PB=PD.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
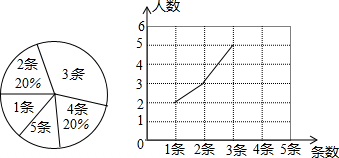
 某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论:
某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论:
 如图,已知直线EF与AB、CD分别相交于点G、H,且∠1=∠3,那么AB与CD平行吗?为什么?
如图,已知直线EF与AB、CD分别相交于点G、H,且∠1=∠3,那么AB与CD平行吗?为什么? 某市出租车管理处公示的出租车运价如图:
某市出租车管理处公示的出租车运价如图: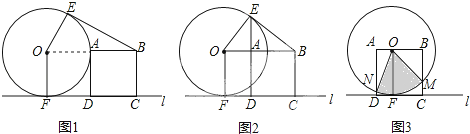
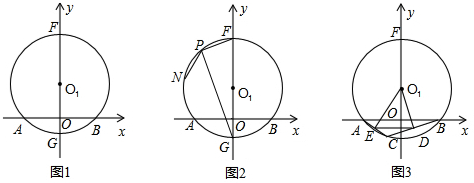
 如图,在平面直角坐标系中,点A、B、C的坐标分别为(2,0)、(1,2)、(3,4),直线l的解析式为:y=kx+4-3k(k≠0).
如图,在平面直角坐标系中,点A、B、C的坐标分别为(2,0)、(1,2)、(3,4),直线l的解析式为:y=kx+4-3k(k≠0).