题目内容
14. 如图,已知在Rt△ABC中,∠C=90°,它的三边长分别为a,b,c,对于同一个角A的正弦,余弦存在关系式sin2A+cos2A=1,试说明.
如图,已知在Rt△ABC中,∠C=90°,它的三边长分别为a,b,c,对于同一个角A的正弦,余弦存在关系式sin2A+cos2A=1,试说明.(1)在横线上填上适当内容;
解:∵sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$.
∴sin2A+cos2A=$\frac{{a}^{2}+{b}^{2}}{c}$,
∵a2+b2=c2,∴sin2A+cos2A=1.
(2)若∠α为锐角,利用(1)的关系式解决下列问题.
①若sinα=$\frac{4}{5}$,求cosα的值;
②若sinα+cosα=$\frac{3}{2}$,求sinαcosα的值.
分析 (1)根据正余弦的定义得到sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,则sin2A+cos2A=$\frac{{a}^{2}+{b}^{2}}{{c}^{2}}$,然后利用勾股定理可得sin2A+cos2A=1;
(2)①利用cosα=$\sqrt{1-si{n}^{2}A}$进行计算;
②把sinα+cosα=$\frac{3}{2}$两边平方得到sin2α+2sinαcosα+cos2α=$\frac{9}{4}$,然后利用sin2α+cos2α=1得到1+2sinαcosα=$\frac{9}{4}$,则易得sinαcosα=$\frac{5}{8}$.
解答 解:(1)∵sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$.
∴sin2A+cos2A=$\frac{{a}^{2}+{b}^{2}}{{c}^{2}}$,
∵a2+b2=c2,
∴sin2A+cos2A=1;
(2)①∵sinα=$\frac{4}{5}$,
∴cosα=$\sqrt{1-si{n}^{2}A}$=$\sqrt{1-(\frac{4}{5})^{2}}$=$\frac{3}{5}$;
②∵sinα+cosα=$\frac{3}{2}$,
∴(sinα+cosα)2=$\frac{9}{4}$,
∴sin2α+2sinαcosα+cos2α=$\frac{9}{4}$,
∵sin2α+cos2α=1,
∴1+2sinαcosα=$\frac{9}{4}$,
∴sinαcosα=$\frac{5}{8}$.
故答案为$\frac{a}{c}$,$\frac{b}{c}$,$\frac{{a}^{2}+{b}^{2}}{{c}^{2}}$.
点评 本题考查了同角三角函数的关系:平方关系:sin2A+cos2A=1;(2)正余弦与正切之间的关系(积的关系):一个角的正切值等于这个角的正弦与余弦的比,即tanA=$\frac{sinA}{cosA}$或sinA=tanA•cosA.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案| A. | 12cm | B. | 15cm | C. | 12或15cm | D. | 18cm或36cm |
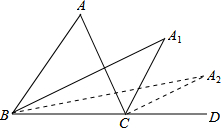 如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2014BC和∠A2014CD的平分线交于点A2015,则∠A2015=$\frac{m}{{2}^{2015}}$度.
如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2014BC和∠A2014CD的平分线交于点A2015,则∠A2015=$\frac{m}{{2}^{2015}}$度.