��Ŀ����
9���۲����и�ʽ����$\frac{1}{2��3}$=$\frac{1}{2}-\frac{1}{3}$����$\frac{1}{3��4}$=$\frac{1}{3}-\frac{1}{4}$����$\frac{1}{4��5}$=$\frac{1}{4}-\frac{1}{5}$����$\frac{1}{5��6}$=$\frac{1}{5}$-$\frac{1}{6}$����1����nΪ���������ú�n�Ĵ���ʽ��ʾ�㷢�ֵĹ��ɣ�
��2���������㷢�ֵĹ�����$\frac{1}{��x-1����x-2��}$+$\frac{1}{��x-2����x-3��}$+$\frac{1}{��x-3����x-4��}$�Ľ����
���� ��1���۲������ʽ�����ݵ�ʽ�ı仯�ҳ��仯���ɡ�$\frac{1}{n��n+1��}$=$\frac{1}{n}$-$\frac{1}{n+1}$��nΪ��������n��0��-1������
��2���Լ���1���ó��Ĺ��ɼ��ɵó����ۣ�
��� �⣺��1���۲죬���ֹ��ɣ�$\frac{1}{2��3}$=$\frac{1}{2}-\frac{1}{3}$��$\frac{1}{3��4}$=$\frac{1}{3}-\frac{1}{4}$��$\frac{1}{4��5}$=$\frac{1}{4}-\frac{1}{5}$��$\frac{1}{5��6}$=$\frac{1}{5}$-$\frac{1}{6}$������
��$\frac{1}{n��n+1��}$=$\frac{1}{n}$-$\frac{1}{n+1}$��n��������n��0��-1����
��2����ϣ�1���Ľ��ۿ�֪��
ԭʽ=$\frac{1}{x-2}-\frac{1}{x-1}$+$\frac{1}{x-3}-\frac{1}{x-2}$+$\frac{1}{x-4}-\frac{1}{x-3}$��
=$\frac{1}{x-4}-\frac{1}{x-1}$��
=$\frac{3}{��x-4����x-1��}$��
���� ���⿼���˹������е����ֵı仯�࣬����Ĺؼ����ҳ��仯���ɡ�$\frac{1}{n��n+1��}$=$\frac{1}{n}$-$\frac{1}{n+1}$��nΪ��������n��0��-1�������������ڻ����⣬�ѶȲ������������Ŀʱ�����ݵ�ʽ�ı仯�ҳ��仯�����ǹؼ���

| A�� | 3a+2b=5ab | B�� | 2a3+3a2=5a5 | C�� | 5a2-4a2=1 | D�� | 5a2b-5ba2=0 |
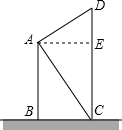 С������С���ҵ���¥���ڣ������10�ף���ͼ��С���ҵ�¥��ABΪ18�ף���С����¥�Ķ���Ŀ��С����ס��¥��CD�ĵײ��붥����������ˮƽ�ߵļнǷֱ�Ϊ55���35�㣬���ܷ����С����ס��¥��CD�ж�ߣ���˵�����ɣ�
С������С���ҵ���¥���ڣ������10�ף���ͼ��С���ҵ�¥��ABΪ18�ף���С����¥�Ķ���Ŀ��С����ס��¥��CD�ĵײ��붥����������ˮƽ�ߵļнǷֱ�Ϊ55���35�㣬���ܷ����С����ס��¥��CD�ж�ߣ���˵�����ɣ�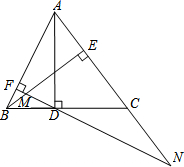 ��ͼ��AD��BE�ǡ�ABC�������ߣ�����D��DF��AB������ΪF��FD��BE��M��FD��AC���ӳ��߽��ڵ�N��
��ͼ��AD��BE�ǡ�ABC�������ߣ�����D��DF��AB������ΪF��FD��BE��M��FD��AC���ӳ��߽��ڵ�N��