��Ŀ����
8�� ��ͼ����ƽ��ֱ��ϵ�У���A��B�ֱ���x�ᡢy���ϣ�A��8��0����B��0��6������P�ӵ�B��������BA��ÿ��1����λ���ٶ����A�˶�����Q�ӵ�A��������AO��ÿ��1����λ���ٶ����O�˶�����P��Qͬʱ����������Q�����Oʱ������ͬʱֹͣ�˶������Q���˶�ʱ��Ϊt�룮
��ͼ����ƽ��ֱ��ϵ�У���A��B�ֱ���x�ᡢy���ϣ�A��8��0����B��0��6������P�ӵ�B��������BA��ÿ��1����λ���ٶ����A�˶�����Q�ӵ�A��������AO��ÿ��1����λ���ٶ����O�˶�����P��Qͬʱ����������Q�����Oʱ������ͬʱֹͣ�˶������Q���˶�ʱ��Ϊt�룮��1������PQ������Q��QC��AO��AB�ڵ�C���ú�t�Ĵ���ʽ��ʾC�����ꣻ
��2���������˶������У���tΪ��ֵʱ����CPQΪ���������Σ�
���� ��1��֤����ACQ�ס�ABO���б���ʽ��CQ�ij�����ʾ��C������Ϊ��8-t��$\frac{3}{4}$t����
��2��������������ۣ�
�ٵ�CP=CQʱ����ͼ1������PC=CQ��ʽ�����
�ڵ�CP=PQʱ����ͼ2����P��PD��CQ��D������AP=$\frac{1}{2}$AC��ʽ�����
�۵�CQ=CPʱ����ͼ3������AP�ij������������㷨��ʽ��
�ܵ�CQ=PQʱ����ͼ4������ͬ�ǵ����Ǻ�����CE��EP�ij�������AC=CP+AP=$\frac{5}{4}$t����ʽ�����
���  �⣺��1��������ã�AQ=BP=t��
�⣺��1��������ã�AQ=BP=t��
��OQ=OA-AQ=8-t��
��CQ��AO��BO��AO��
��CQ��BO��
���ACQ�ס�ABO��
��$\frac{CQ}{BO}=\frac{AQ}{AO}$��
��$\frac{CQ}{6}=\frac{t}{8}$��
��CQ=$\frac{3}{4}$t��
��C��8-t��$\frac{3}{4}$t����
��2���ٵ�CP=CQʱ����ͼ1��
��Rt��ACQ��AC=$\sqrt{C{Q}^{2}+A{Q}^{2}}$=$\sqrt{��\frac{3}{4}t��^{2}+{t}^{2}}$=$\frac{5}{4}$t��
��Rt��AOB��AB=10��
��PC=AB-PB-AC=10-t-$\frac{5}{4}$t��
��$\frac{3}{4}$t=10-t-$\frac{5}{4}$t��
t=$\frac{10}{3}$��
�ڵ�CP=PQʱ����ͼ2����P��PD��CQ��D��
��CD=DQ��
��PD��AQ��
��CP=PA��
�ɢٵã�AC=$\frac{5}{4}$t��
��AP=$\frac{1}{2}$AC=$\frac{5}{8}$t��
��$\frac{5}{8}t$=10-t��
t=$\frac{80}{13}$��
�۵�CQ=CPʱ����ͼ3��
��CQ=CP=$\frac{3}{4}$t��
��AP=AC-CP=$\frac{5}{4}$t-$\frac{3}{4}$t=$\frac{t}{2}$��
��$\frac{t}{2}$=10-t��
t=$\frac{20}{3}$��
�ܵ�CQ=PQʱ����ͼ4��
��Q��QE��AB��E��
cos��QCA=cos��OBA��
��$\frac{BO}{AB}=\frac{CE}{CQ}$��
��$\frac{6}{10}=\frac{CE}{\frac{3}{4}t}$��
��CE=$\frac{9}{20}t$��
��CE=PE=$\frac{9}{20}t$��
��AC=CP+AP=$\frac{5}{4}$t��
��$\frac{9}{20}t$+$\frac{9}{20}t$+10-t=$\frac{5}{4}$t��
t=$\frac{200}{27}$��
������������tΪ$\frac{10}{3}$��$\frac{80}{13}$��$\frac{20}{3}$��$\frac{200}{27}$ʱ����CPQΪ���������Σ�
���� ���⿼���˵��������ε����ʺ��ж���������ͼ�����ʡ����������Ƶ����ʺ��ж������Ǻ����ȣ����ڶ������⣬Ҫ��ȷ�������·�ߡ��ٶȡ�ʱ�䣬ȷ����·���ǹؼ�������ʾ��Ӧ�߶εij����������˷������۵�˼��ȷ������������ʱt��ʱ�䣬��������©�⣬Ҫȫ���濼�ǣ�

 �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�| A�� | $sin{60��}=\frac{1}{2}$ | B�� | $tan{60��}=\sqrt{3}$ | C�� | $sin{45��}=\frac{{\sqrt{3}}}{2}$ | D�� | $cos{30��}=\frac{1}{2}$ |
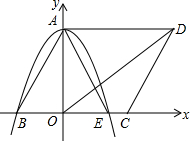 ��ͼ����ƽ��ֱ������ϵ�У��ı���ABCD��ƽ���ı��Σ��߶�AD=6�����κ���y=-$\frac{1}{2}$x2-$\frac{1}{6}$x+4��y�ύ��A�㣬��x��ֱ���B�㡢E�㣨B����E�����ࣩ
��ͼ����ƽ��ֱ������ϵ�У��ı���ABCD��ƽ���ı��Σ��߶�AD=6�����κ���y=-$\frac{1}{2}$x2-$\frac{1}{6}$x+4��y�ύ��A�㣬��x��ֱ���B�㡢E�㣨B����E�����ࣩ