Question

20．已知点O是直线AB上的一点，∠COE=90°，OF是∠AOE的平分线．
（1）当点C、E、F在直线AB的同侧（如图1所示）
①若∠COF=25°，则∠BOE=50°．
②猜想∠COF与∠BOE的数量关系是∠BOE=2∠COF．
（2）当点C与点E、F在直线AB的两旁（如图2所示）时，（1）中第②式的结论是否仍然成立？请给出你的结论并说明理由．

Answer 1

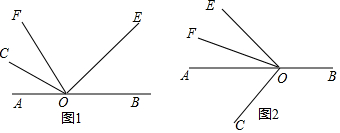
分析 （1）根据角平分线的定义得到∠EOF=$\frac{1}{2}$∠AOE，而∠EOF=90°-∠COF，即90°-∠COF=$\frac{1}{2}$∠AOE，再根据邻补角的定义得到90°-∠COF=$\frac{1}{2}$（180°-∠BOE），整理得∠BOE=2∠COF；所以①当∠COF=25°时，∠BOE=2×25°=50°；②当∠COF=α时，∠BOE=2α；
（2）第②式的结论仍然成立．证明方法与前面一样．

解答 27、解：（1）∵OF是∠AOE的平分线，
∴∠EOF=$\frac{1}{2}$∠AOE，
∵∠COE=90°，
∴∠EOF=90°-∠COF，
∴90°-∠COF=$\frac{1}{2}$∠AOE，
而∠AOE+∠BOE=180°，
∴90°-∠COF=$\frac{1}{2}$（180°-∠BOE），
∴∠BOE=2∠COF，
①当∠COF=25°时，∠BOE=2×25°=50°；
②当∠COF=α时，∠BOE=2α；
故答案为2α；（1）①50°，
②∠BOE=2∠COF；

（2）第②式的结论仍然成立．理由如下：
∵OF是∠AOE的平分线，
∴∠EOF=$\frac{1}{2}$∠AOE，
∵∠COE=90°，
∴∠EOF=90°-∠COF，
∠AOE+∠BOE=180°，
∴90°-∠COF=$\frac{1}{2}$（180°-∠BOE），
∴∠BOE=2∠COF．

点评 本题主要考查的是角的计算、补角和余角的定义，依据余角和邻补角的定义求得∠EOF和∠BOE的度数是解题的关键．