题目内容
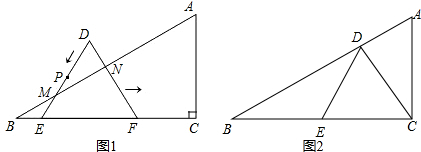
19. 如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果$\frac{AD}{BC}=\frac{1}{4}$,那么$\frac{AF}{BF}$的值是( )
如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果$\frac{AD}{BC}=\frac{1}{4}$,那么$\frac{AF}{BF}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 根据对称的性质得到△BFE≌△DFE,得到DE=BE.根据已知条件得到∠DEB=90°,设AD=1,BC=4,过A作AG⊥BC于G,根据矩形的性质得到GE=AD=1,根据全等三角形的性质得到BG=EC=1.5,根据勾股定理得到AB=CD=$\sqrt{A{G}^{2}+B{G}^{2}}$=5$\sqrt{34}$,通过△BDC∽△DEF,得到$\frac{DF}{CD}=\frac{DE}{BC}$,求出BF=$\frac{25\sqrt{34}}{8}$,于是得到结论.
解答 解:∵EF是点B、D的对称轴,
∴△BFE≌△DFE,
∴DE=BE.
∵在△BDE中,DE=BE,∠DBE=45°,
∴∠BDE=∠DBE=45°.
∴∠DEB=90°,
∴DE⊥BC.
在等腰梯形ABCD中,∵$\frac{AD}{BC}=\frac{1}{4}$,
∴设AD=1,BC=4,
过A作AG⊥BC于G,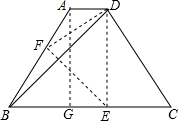
∴四边形AGED是矩形.
∴GE=AD=1,
∵Rt△ABG≌Rt△DCE,
∴BG=EC=1.5,
∴AG=DE=BE=2.5
∴AB=CD=$\sqrt{A{G}^{2}+B{G}^{2}}$=5$\sqrt{34}$,
∵∠ABC=∠C=∠FDE,
∵∠CDE+∠C=90°,
∴∠FDE+∠CDE=90°
∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°,
∴∠BDC=∠DFE,
∵∠DEF=∠DBC=45°,
∴△BDC∽△DEF,
∴$\frac{DF}{CD}=\frac{DE}{BC}$,
∴DF=$\frac{25\sqrt{34}}{8}$,
∴BF=$\frac{25\sqrt{34}}{8}$,
∴AF=AB-BF=$\frac{15\sqrt{34}}{8}$,
∴$\frac{AF}{BF}$=$\frac{3}{5}$.
故选B.
点评 此题考查等腰梯形的性质,翻折的性质,三角形全等的判定与性质,等腰直角三角形的性质,相似三角形的判定和性质等知识,注意结合图形,作出常用辅助线解决问题.

 高中必刷题系列答案
高中必刷题系列答案①每个命题都有逆命题;②互逆命题的真假性一致;③每个定理都有逆定理.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | m$<\frac{1}{4}$ | B. | m$≤\frac{1}{4}$ | C. | m$≥\frac{1}{4}$ | D. | m$≤\frac{1}{4}$且m≠0 |
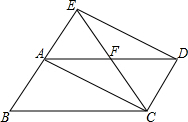 如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是( )
如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是( )| A. | AF=$\frac{1}{2}BC$ | B. | 四边形ACDE是矩形 | ||
| C. | 图中与△ABC全等的三角形有4个 | D. | 图中有4个等腰三角形 |
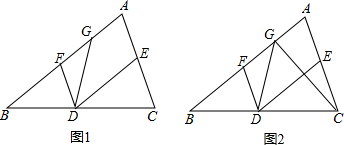
 已知:如图,等边△ABC中AB=AC=BC=6,请画出△ABC的外接圆⊙O,(要求保留作图痕迹),并计算此外接圆的半径r.
已知:如图,等边△ABC中AB=AC=BC=6,请画出△ABC的外接圆⊙O,(要求保留作图痕迹),并计算此外接圆的半径r.