Question

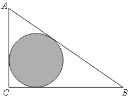
【题目】如图，已知AB是⊙O的直径，C是⊙O上的点，点D在AB的延长线上，∠BCD=∠BAC.

（1）求证：CD是⊙O的切线．

（2）若∠D=30°，BD=2，求⊙O的半径

（3）在（2）的条件下，求图中阴影部分的面积．

Answer 1

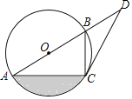
【答案】（1）见解析；（2）2；（3）

【解析】

（1）连接OC,则得∠BAC=∠OCA，结合条件∠BCD=∠BAC证出∠OCD=90°,得OC⊥CD则可证切线；

（2）在Rt△OCD中，利用30°角所对的直角边等于斜边的一半可得OD与半径的关系，列方程求解；

（3）根据弓形面积等于扇形面积减去三角形的面积，分别用公式计算扇形和三角形的面积即可求解.

解：如图，连接

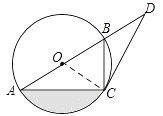
（1）∵OA=OC，

∴∠BAC=∠OCA,

∵∠BCD=∠BAC,

∴,

∵是直径，

∴∠ACB=90°=∠OCA+∠OCB,

∴，即.

∵是半径，

∴CD是⊙O的切线.

（2）设⊙O的半径为r，则,

∵，，

∴，，

由OB+BD=OD得，

解得，

∴⊙O的半径为2.

（3）在中，∵∠BOC=60°，

∴是正三角形，

∵OB=OC=2

∴由勾股定理得.

∵O为中点，

∴.

∵，

∴，

所以，

所以.

故图中阴影部分的面积为.