题目内容
15.若x1、x2是一元二次方程(x-3)(x-4)=2的两个解,则|x1-x2|的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先把方程化为一般式,再根据根与系数的关系得到x1+x2=7,x1x2=10,然后利用完全平方公式得到|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,再利用整体代入的方法计算即可.
解答 解:(x-3)(x-4)=2化为一般是为x2-7x+10=0,
x1+x2=7,x1x2=10,
所以|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{{7}^{2}-4×10}$=3.
故选C.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
5.下列各曲线中,哪些表示y是x的函数( )


| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
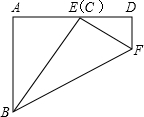 在一次数学课上,小明同学把一个宽为3(AB=3)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的长AD.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)
在一次数学课上,小明同学把一个宽为3(AB=3)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的长AD.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19) 如图,已知DE∥BC,S△ADE=9,AD=3,BD=2,那么S△ABC=9.
如图,已知DE∥BC,S△ADE=9,AD=3,BD=2,那么S△ABC=9.