题目内容
3.若分式方程$\frac{x-2}{x-3}-2=\frac{m}{x-3}$有增根,则m的值为( )| A. | -1 | B. | 1 | C. | 0 | D. | 以上都不对 |
分析 增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x-3)=0,得到x=3,然后代入化为整式方程的方程算出a的值.
解答 解:方程两边都乘(x-3),
得x-2-2(x-3)=m
∵原方程有增根,
∴最简公分母(x-3)=0,
解得x=3,
当x=3时,m=1.
故选:B.
点评 本题考查了分式方程的增根,增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知点P(a,b)是平面直角坐标系中第四象限的点,则化简$\sqrt{b^2}$+|b-a|的结果是( )
| A. | a-2b | B. | a | C. | -a+2b | D. | -a |
18.弹簧挂上物体后会伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表:
(1)上表反映的变量之间的关系中自变量是物体的质量,因变量是弹簧的长度.
(2)当所挂物体是3kg时,弹簧的长度是13.5cm,不挂重物是12cm.
(3)直接写出y与x的关系式,并求出当弹簧长度为17cm时所挂物体质量.
| 物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度y(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(2)当所挂物体是3kg时,弹簧的长度是13.5cm,不挂重物是12cm.
(3)直接写出y与x的关系式,并求出当弹簧长度为17cm时所挂物体质量.
8.下列各式中计算正确的是( )
| A. | $\sqrt{-4}$$\sqrt{-16}$=(-2)(-4)=8 | B. | $\sqrt{8{a^2}}=4a(a>0)$ | C. | $\sqrt{{3^2}+{4^2}}=3+4=7$ | D. | ($\sqrt{3}$+2)2=7+4$\sqrt{3}$ |
15.在平面直角坐标系中,点(-3,-2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.下列命题中,真命题是( )
| A. | 两条对角线垂直且相等的四边形是正方形 | |
| B. | 两条对角线互相垂直的四边形是菱形 | |
| C. | 两条对角线互相平分且相等的四边形是矩形 | |
| D. | 一组对边平行,另一组对边相等的四边形是平行四边形 |
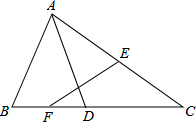 如图,在△ABC中,D是BC上一点,AB=AD,E、F分别是AC、BD的中点,EF=2,则AC的长是( )
如图,在△ABC中,D是BC上一点,AB=AD,E、F分别是AC、BD的中点,EF=2,则AC的长是( )