题目内容
11.已知点P(a,b)是平面直角坐标系中第四象限的点,则化简$\sqrt{b^2}$+|b-a|的结果是( )| A. | a-2b | B. | a | C. | -a+2b | D. | -a |
分析 根据第四象限的点的横坐标是正数,纵坐标是负数,求解即可.
解答 解:∵点P(a,b)是平面直角坐标系中第四象限的点,
∴a>0,b<0,
∴b-a<0,
∴$\sqrt{b^2}$+|b-a|=-b-(b-a)=-b-b+a=-2b+a=a-2b,
故选:A.
点评 本题考查了点的坐标,解决本题的关键是明确第四象限的点的横坐标是正数,纵坐标是负数.

练习册系列答案
相关题目
3.若分式方程$\frac{x-2}{x-3}-2=\frac{m}{x-3}$有增根,则m的值为( )
| A. | -1 | B. | 1 | C. | 0 | D. | 以上都不对 |
20.若分式$\frac{3}{x-2}$有意义,则x应满足的条件是( )
| A. | x≠0 | B. | x≥2 | C. | x≠2 | D. | x≤2 |
1.若x>y,则下列式子错误的是( )
| A. | x-3>y-3 | B. | -x>-y | C. | x+3>y+2 | D. | $\frac{x}{3}$>$\frac{y}{3}$ |

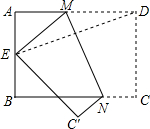 如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.
如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.