题目内容
20.计算:(1)$\sqrt{3}$×(-$\sqrt{6}$)+|-2$\sqrt{2}$|+($\frac{1}{2}$)-3
(2)$\frac{\sqrt{18×12}}{\sqrt{32}}$-$\frac{\sqrt{27}}{4}$.
分析 (1)利用二次根式的乘法法则和负整数指数幂的意义计算;
(2)利用二次根式的乘除法则运算,然后化简后合并即可.
解答 解:(1)原式=-$\sqrt{3×6}$+2$\sqrt{2}$+8
=-3$\sqrt{2}$+2$\sqrt{2}$+8
=8-$\sqrt{2}$;
(2)原式=$\sqrt{\frac{18×12}{32}}$-$\frac{3\sqrt{3}}{4}$
=$\frac{3\sqrt{3}}{2}$-$\frac{3\sqrt{3}}{4}$
=$\frac{3\sqrt{3}}{4}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
10.若a=b,下列等式不一定成立的是( )
| A. | a-5=b-5 | B. | a+3=b+3 | C. | 2a=2b | D. | $\frac{a}{c}$=$\frac{b}{c}$ |
11.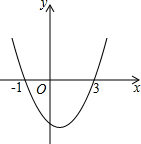 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )
 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
15. 我国古代数学家赵爽的《勾股方圆图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是16,小正方形的面积是3,直角三角形较短的直角边为a,较长的直角边为b那么(a+b)2的值为( )
我国古代数学家赵爽的《勾股方圆图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是16,小正方形的面积是3,直角三角形较短的直角边为a,较长的直角边为b那么(a+b)2的值为( )
 我国古代数学家赵爽的《勾股方圆图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是16,小正方形的面积是3,直角三角形较短的直角边为a,较长的直角边为b那么(a+b)2的值为( )
我国古代数学家赵爽的《勾股方圆图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是16,小正方形的面积是3,直角三角形较短的直角边为a,较长的直角边为b那么(a+b)2的值为( )| A. | 16 | B. | 29 | C. | 19 | D. | 48 |
8.随着科技技术的不断发展,网上购物越来越便捷,它已成为人们生活的一部分,去年双十一,淘宝天猫的销售额就高达912.17亿元用科学记数法表示为( )
| A. | 9.1217×1010 | B. | 9.1217×109 | C. | 0.91217×103 | D. | 0.91217×102 |
 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,求证:DE=DB.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,求证:DE=DB.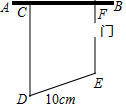 张大伯利用一堵旧墙AB,用长50m的篱笆围成一个留有1m宽的门的梯形场地CDEF(CD∥EF),如图所示,若DE的长为10m,则梯形场地CDEF的最大面积是多少?
张大伯利用一堵旧墙AB,用长50m的篱笆围成一个留有1m宽的门的梯形场地CDEF(CD∥EF),如图所示,若DE的长为10m,则梯形场地CDEF的最大面积是多少?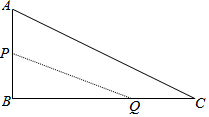 如图,在△ABC中,∠B=90°,AB=6mm,BC=12mm,动点P从点A开始沿边AB向点B以1mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向点C以2mm/s的速度移动(不与点C重合),如果P,Q分别从A,B同时出发,那么经过3秒,四边形APQC的面积最小.
如图,在△ABC中,∠B=90°,AB=6mm,BC=12mm,动点P从点A开始沿边AB向点B以1mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向点C以2mm/s的速度移动(不与点C重合),如果P,Q分别从A,B同时出发,那么经过3秒,四边形APQC的面积最小.