题目内容
13.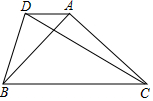 如图,在△ABC中,∠BAC=90°,AB=AC,DA∥BC,tan∠DBA=$\frac{1}{2}$,若CD=2$\sqrt{17}$,则线段BC的长为,6$\sqrt{2}$.
如图,在△ABC中,∠BAC=90°,AB=AC,DA∥BC,tan∠DBA=$\frac{1}{2}$,若CD=2$\sqrt{17}$,则线段BC的长为,6$\sqrt{2}$.
分析 过D作DE⊥AB于E,DF⊥BC于F,根据等腰直角三角形的性质得到∠ABC=45°,根据平行线的性质得到∠DAE=∠ABC=45°,设AE=DE=x,由tan∠DBA=$\frac{1}{2}$,得到BE=2x,根据勾股定理得到BD=$\sqrt{5}$x,AB=AC=3x,求得BC=3$\sqrt{2}$x,根据勾股定理得到DF2+CF2=CD2,即($\frac{3\sqrt{2}}{2}$x)2+($\frac{5\sqrt{2}}{2}$x)2=(2$\sqrt{17}$)2,于是得到结论.
解答 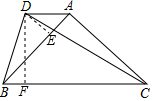 解:过D作DE⊥AB于E,DF⊥BC于F,
解:过D作DE⊥AB于E,DF⊥BC于F,
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∵DA∥BC,
∴∠DAE=∠ABC=45°,
∴AE=DE,
设AE=DE=x,
∵tan∠DBA=$\frac{1}{2}$,
∴BE=2x,
∴BD=$\sqrt{5}$x,AB=AC=3x,
∴BC=3$\sqrt{2}$x,
∴DF=$\frac{3\sqrt{2}}{2}$x,
∴BF=$\frac{\sqrt{2}}{2}$x,
∴CF=$\frac{5\sqrt{2}}{2}$x,
∵DF2+CF2=CD2,
∴($\frac{3\sqrt{2}}{2}$x)2+($\frac{5\sqrt{2}}{2}$x)2=(2$\sqrt{17}$)2,
∴x=2,
∴BC=6$\sqrt{2}$.
故答案为:6$\sqrt{2}$,
点评 本题考查了解直角三角形,梯形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,求证:DE=DB.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,求证:DE=DB.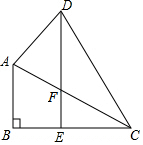 如图,在四边形ABCD中,∠B=90°,DE∥AB交BC于E、交AC于F,∠CDE=∠ACB=30°,BC=DE.求证:△FCD是等腰三角形.
如图,在四边形ABCD中,∠B=90°,DE∥AB交BC于E、交AC于F,∠CDE=∠ACB=30°,BC=DE.求证:△FCD是等腰三角形.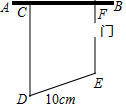 张大伯利用一堵旧墙AB,用长50m的篱笆围成一个留有1m宽的门的梯形场地CDEF(CD∥EF),如图所示,若DE的长为10m,则梯形场地CDEF的最大面积是多少?
张大伯利用一堵旧墙AB,用长50m的篱笆围成一个留有1m宽的门的梯形场地CDEF(CD∥EF),如图所示,若DE的长为10m,则梯形场地CDEF的最大面积是多少?