题目内容
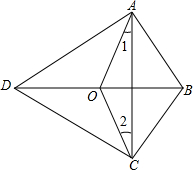如图，在四边形ABCD中，∠BAD=∠BCD=90°，点O是BD的中点．求证：∠1=∠2．考点：直角三角形斜边上的中线,等腰三角形的判定与性质
专题：证明题
分析：根据直角三角形斜边上中线性质求出BD=2AO，BD=2CO，推出AO=CO，根据等腰三角形的判定推出即可．
解答：证明：∵∠BAD=∠BCD=90°，点O是BD的中点，
∴BD=2AO，BD=2CO，
∴AO=CO，
∴∠1=∠2．
∴BD=2AO，BD=2CO，
∴AO=CO，
∴∠1=∠2．
点评：本题考查了直角三角形斜边上中线性质和等腰三角形的判定的应用，解此题的关键是根据性质得出AO=CO，注意：直角三角形斜边上的中线等于斜边的一半，等边对等角．
练习册系列答案
百年学典课时学练测系列答案
相关题目
如图，已知⊙O的半径为2cm，弦AB=2cm，P点为弦AB上一动点，则线段OP的范围是身高相同的甲、乙、丙三人放风筝，各人放出线长分别为300米、350米、280米，线与地面的夹角分别为30°、45°、60°（假设风筝线是拉直的），三人所放风筝（ ）
| A、甲的最高 | B、乙的最高 |
| C、丙的最高 | D、一样高 |
四边形ABCD的对角线AC、BD相交于点O，且AD∥BC，AD=BC，补上下列条件中①AC=BD；②AB=AD；③AB=CD；④AC⊥BD，能使四边形ABCD为正方形的是（ ）
| A、①② | B、②③ |
| C、③④ | D、①②或①④ |
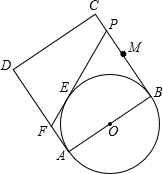已知正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点，P不与M和C重合，以AB为直径作⊙O，过点P作⊙O的切线交AD于点F，切点为E．求四边形CDFP的周长．
在直角坐标系中，等腰直角三角形A1B1O、A2B2B1、A3B3B2、…、AnBnBn-1按如图所示的方式放置，其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上，点B1、B2、B3、…、Bn均在x轴上．若点B1的坐标为（1，0），点B2的坐标为（3，0），则点An的坐标为（ ）| A、（2n-1，2n-1） |
| B、（2n-1，2n-1-1） |
| C、（2n-1，2n-1+1） |
| D、（2n-1-1，2n-1） |