题目内容
将一个长方体纸片的四角各裁去一个小正方体,做成一个无盖的长方体纸盒.要求成纸盒的容积为2000cm3,长、宽、高之比为2:1:1,库存的纸板材料有20×60,80×40,60×80,90×30几种尺寸(单位:cm).请问选择哪一种材料合适?为什么?
考点:立方根
专题:
分析:根据长方体的体积公式得到纸盒的长、宽、高,依此即可求解.
解答:解:设纸盒的长是2xcm、宽是xcm、高是xcm,依题意有
2x3=2000,
解得x=10,
则2x=2×10=20,
∵20+10×2=40(cm),
10+10×2=30(cm),
∴选择60×80尺寸的材料合适.
2x3=2000,
解得x=10,
则2x=2×10=20,
∵20+10×2=40(cm),
10+10×2=30(cm),
∴选择60×80尺寸的材料合适.
点评:此题主要考查了利用立方根的定义解决实际问题,关键是熟练掌握长方体的体积公式.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
若25x2-40xy+m是一个完全平方式,那么m的值是( )
| A、4y2 |
| B、±4y2 |
| C、±16y2 |
| D、16y2 |
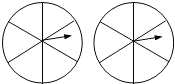 如图,用两个相同的转盘(每个圆都平均分成六个扇形)玩配紫色游戏(-个转盘转出“红”,另一个转盘转出“蓝”,则为配成紫色).在所给转盘中的扇形里,分别填上“红”或“蓝”,使得到紫色的概率是
如图,用两个相同的转盘(每个圆都平均分成六个扇形)玩配紫色游戏(-个转盘转出“红”,另一个转盘转出“蓝”,则为配成紫色).在所给转盘中的扇形里,分别填上“红”或“蓝”,使得到紫色的概率是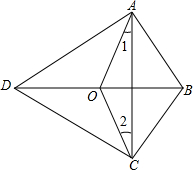 如图,在四边形ABCD中,∠BAD=∠BCD=90°,点O是BD的中点.求证:∠1=∠2.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,点O是BD的中点.求证:∠1=∠2.