题目内容
四边形ABCD的对角线AC、BD相交于点O，且AD∥BC，AD=BC，补上下列条件中①AC=BD；②AB=AD；③AB=CD；④AC⊥BD，能使四边形ABCD为正方形的是（ ）
| A、①② | B、②③ |
| C、③④ | D、①②或①④ |
考点：正方形的判定
专题：
分析：因为AD∥BC，AD=BC，所以四边形ABCD为平行四边形，添加①则可根据对角线相等的平行四边形是矩形，证明四边形是矩形，故可根据一组邻边相等的矩形是正方形来添加条件．
解答：解：∵AD∥BC，AD=BC
∴四边形ABCD为平行四边形
∵AC=BD
∴平行四边形ABCD是矩形
若AB=AD
则四边形ABCD为正方形；
若AC⊥BD，则四边形ABCD是正方形．
故选：D．
∴四边形ABCD为平行四边形
∵AC=BD
∴平行四边形ABCD是矩形
若AB=AD
则四边形ABCD为正方形；
若AC⊥BD，则四边形ABCD是正方形．
故选：D．
点评：本题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念，途经有两种：
①先说明它是矩形，再说明有一组邻边相等；
②先说明它是菱形，再说明它有一个角为直角．
①先说明它是矩形，再说明有一组邻边相等；
②先说明它是菱形，再说明它有一个角为直角．
练习册系列答案
相关题目
已知
和
都是关于x，y的方程ax-y+b=0的解，则a，b的值是（ ）
|
|
A、a=-
| ||
B、a=-
| ||
C、a=
| ||
D、a=-
|
若25x2-40xy+m是一个完全平方式，那么m的值是（ ）
| A、4y2 |
| B、±4y2 |
| C、±16y2 |
| D、16y2 |
已知x有两个平方根，且|x|=4，则x的值是（ ）
| A、4 | B、16 | C、2 | D、±4 |
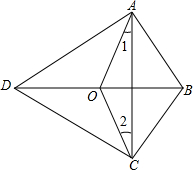如图，在四边形ABCD中，∠BAD=∠BCD=90°，点O是BD的中点．求证：∠1=∠2．