题目内容
14.在△ABC中,∠C=90°,c=25cm,a:b=3:4,则S△ABC=150cm2.分析 设a=3xcm,则b=4xcm,由勾股定理得出方程,解方程求出a、b,S△ABC=$\frac{1}{2}$ab,即可得出结果.
解答 解:设a=3xcm,则b=4xcm,
∵∠C=90°,
∴a2+b2=c2,
即(3x)2+(4x)2=252,
解得:x=±5(负值舍去),
∴x=5,
∴a=3×5=15(cm),b=4×5=20(cm),
∴S△ABC=$\frac{1}{2}$ab=$\frac{1}{2}$×15×20=150(cm2);
故答案为:150cm2.
点评 本题考查了勾股定理、直角三角形面积的计算方法、解方程;熟练掌握勾股定理,由勾股定理得出方程求出a、b是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
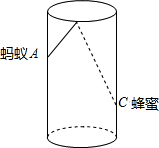 如图,圆柱形玻璃杯,高为8cm,底面周长为12cm,在杯内离杯底2cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,求蚂蚁到达蜂蜜的最短距离.
如图,圆柱形玻璃杯,高为8cm,底面周长为12cm,在杯内离杯底2cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,求蚂蚁到达蜂蜜的最短距离. 如图,已知AB⊥MN,CD⊥MN,垂足分别为E,F.求证:AB∥CD.
如图,已知AB⊥MN,CD⊥MN,垂足分别为E,F.求证:AB∥CD.