题目内容
12. 已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的 交点Q的纵坐标为4.
已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的 交点Q的纵坐标为4.(1)求这两个函数的解析式;
(2)根据已知条件,在同一坐标系中,分别画出这两个函数的图象;
(3)求△PQO的面积.
分析 (1)根据P(-2、2)和一次函数的图象与y轴的交点Q的纵坐标为4,用待定系数法求出解析式;
(2)根据函数解析式,利用函数图象的画法画出函数图象;
(3)求出三角形的底和高,运用三角形的面积公式求出面积.
解答  解:(1)设正比例函数为y=k1x( k1≠0).
解:(1)设正比例函数为y=k1x( k1≠0).
一次函数为y=k2x+b( k2≠0,b≠0).
将P(-2、2)代入y=k1x,则k1=-1.∴y=-x.
将P(-2、2)代入y=k2x+b,则2=-2k2+b.
又一次函数图象与y轴的交点纵坐标为4,
∵b=4,∴2=-2k2+4,则k2=1.∴y=x+4为所求的一次函数;
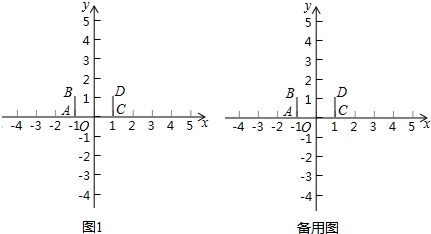
(2)如图,
(3)P到y轴的距离为点P的横坐标的绝对值,即高h=2,底PO=4
所以三角形POQ的面积为S=$\frac{1}{2}×$2×4=4.
点评 本题考查的是待定系数法求函数解析式和函数图象的画法,灵活运用待定系数法求解析式是解题的关键,注意数形结合思想的运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
3.如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,保持上述运动过程,经过$({2015,\sqrt{3}})$的正六边形的顶点是( )

| A. | C或E | B. | B或D | C. | A或C | D. | B或F |
2.下列图案中既是轴对称图形又是中心对称图形的是( )
| A. | 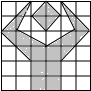 | B. | 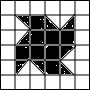 | C. | 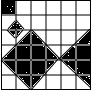 | D. |  |
 已知:△ABC.
已知:△ABC.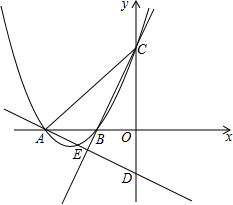 如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,
如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,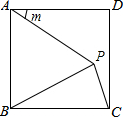 如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为30°或60°或150°或300°.
如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为30°或60°或150°或300°.