题目内容
6.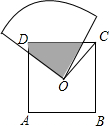 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )
如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )| A. | $\frac{1}{3}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{1}{2}$a2 | D. | $\frac{1}{4}$a |
分析 扇形的半径交AD于E,交CD于F,连结OD,如图,利用正方形的性质得OD=OC,∠COD=90°,∠ODA=∠OCD=45°,再利用等角的余角相等得到∠EOD=∠FOC,于是可证明△ODE≌△OCF,得到S△ODE=S△OCF,所以S阴影部分=S△DOC=$\frac{1}{4}$S正方形ABCD=$\frac{1}{4}$a2.
解答 解:扇形的半径交AD于E,交CD于F,连结OD,如图,
∵四边形ABCD为正方形,
∴OD=OC,∠COD=90°,∠ODA=∠OCD=45°,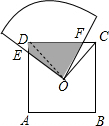
∵∠EOF=90°,即∠EOD+∠DOF=90°,
∠DOF+∠COF=90°,
∴∠EOD=∠FOC,
在△ODE和△OCF中,
$\left\{\begin{array}{l}{∠ODE=∠OCF}\\{OD=OC}\\{∠EOD=∠COF}\end{array}\right.$,
∴△ODE≌△OCF,
∴S△ODE=S△OCF,
∴S阴影部分=S△DOC=$\frac{1}{4}$S正方形ABCD=$\frac{1}{4}$a2.
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
13.将分式$\frac{5x-5y}{x+y}$中的x、y的值同时扩大为原来的2倍,则分式的值( )
| A. | 扩大为原来的2倍 | B. | 缩小为原来的$\frac{1}{2}$ | C. | 扩大为原来的5倍 | D. | 保持不变 |
11.用下列图形不能进行平面镶嵌的是( )
| A. | 正三角形和正四边形 | B. | 正三角形和正六边形 | ||
| C. | 正四边形和正八边形 | D. | 正四边形和正十二边形 |
15.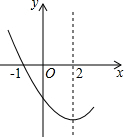 如图是抛物线y=ax2+bx+c(a≠0)图象的一部分.当y<0时,自变量x的范围是( )
如图是抛物线y=ax2+bx+c(a≠0)图象的一部分.当y<0时,自变量x的范围是( )
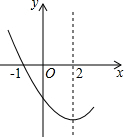 如图是抛物线y=ax2+bx+c(a≠0)图象的一部分.当y<0时,自变量x的范围是( )
如图是抛物线y=ax2+bx+c(a≠0)图象的一部分.当y<0时,自变量x的范围是( )| A. | x<-1或x>2 | B. | x<-1或x>5 | C. | -1<x<5 | D. | -1<x<2 |
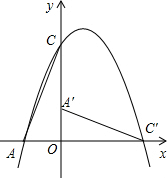 如图,在直角坐标系中,O是坐标原点,点C的坐标是(0,3),抛物线y=-x2+2x+c经过点C,交x轴负半轴于点A.
如图,在直角坐标系中,O是坐标原点,点C的坐标是(0,3),抛物线y=-x2+2x+c经过点C,交x轴负半轴于点A.