题目内容
16．
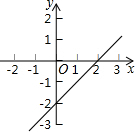如图所示，是函数y=kx+b的图象，利用图象解答：（1）当x为何值时，y=0？
（2）当x为何值时，y＞0？
（3）当x为何值时，y＜0？
（4）当y为何值时，x＞0？
（5）求方程kx+b=0的解．
（6）求方程kx+b=-2的解．
分析 （1）y=0时x的值为直线与x轴交点横坐标；
（2）y＞0时x的范围是直线位于x轴上方的图象对应x的范围；
（3）y＜0时x的范围是直线位于x轴下方的图象对应x的范围；
（4）x＞0时y的范围时直线位于y轴右侧的图象对应的x的取值范围；
（5）用待定系数法求出函数关系式，根据题意列出方程，解方程可得；
（6）根据直线解析式列出方程，解方程可得．
解答 解：由图象可知，（1）当x=2时，y=0；
（2）当x＞2时，y＞0；
（3）当x＜2时，y＜0；
（4）当y＞-2时，x＞0；
（5）将点（0，-2），（2，0）代入y=kx+b，
得：$\left\{\begin{array}{l}{b=-2}\\{2k+b=0}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$，
故直线解析式为：y=x-2，
根据题意，知：x-2=0，解得：x=2；
（6）根据题意，得：x-2=-2，解得：x=0．
点评 本题主要考查一次函数的图象与待定系数法求函数解析式，明确一次函数与一元一次不等式、一元一次方程之间关系是关键．
练习册系列答案
相关题目
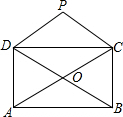如图，矩形ABCD的对角线相交于点O，PD∥AC，PC∥BD．
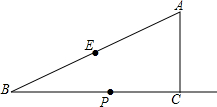如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，E为斜边AB的中点，点P是射线BC上的一个动点，连接AP、PE，将△AEP沿着边PE折叠，折叠后得到△EPA′，当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一，则此时BP的长为2或2$\sqrt{3}$．
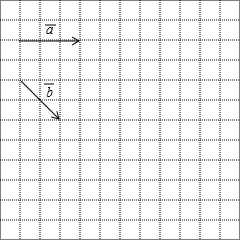如图，在正方形网格中，每一个小正方形的边长都是1，已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的起点、终点都是小正方形的顶点，如果$\overrightarrow{c}$=3$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$，求作$\overrightarrow{c}$并写出$\overrightarrow{c}$的模（不用写作法，只要所求作向量）．