题目内容
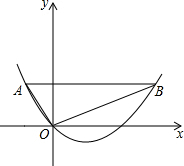 如图,在平面直的坐标角坐标系中,已知点A为(-1,
如图,在平面直的坐标角坐标系中,已知点A为(-1,| 3 |
| 3 |
(1)求m的值;
(2)求过点O,A,B三点的抛物线的解析式,并写出抛物线顶点坐标.
考点:待定系数法求二次函数解析式
专题:
分析:(1)根据题意,过点A作AF⊥x轴,垂足为点F,过点B作BE⊥x轴,垂足为点E;根据相似三角形的性质,即可得m的值;
(2)先设抛物线为y=ax2+bx+c,将ABC的坐标代入可得三元一次方程组,解即可得abc的值,即可得抛物线的解析式;
(2)先设抛物线为y=ax2+bx+c,将ABC的坐标代入可得三元一次方程组,解即可得abc的值,即可得抛物线的解析式;
解答: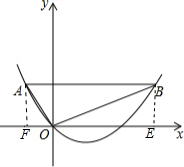 解:(1)过点A作AF⊥x轴,垂足为点F,
解:(1)过点A作AF⊥x轴,垂足为点F,
过点B作BE⊥x轴,垂足为点E,则AF=
,OF=1.
∵OA⊥OB,
∴∠AOF+∠BOE=90°.
又∵∠BOE+∠OBE=90°,
∴∠AOF=∠OBE,
∴Rt△AFO∽Rt△OEB,
∴
=
,
∴
=
,解得m=3.
(2)设过点A(-1,
),B(3,
),O(0,0)的抛物线为y=ax2+bx+c.
∴
,解之,得
,
∴所求抛物线的表达式为y=
x2-
x.
 解:(1)过点A作AF⊥x轴,垂足为点F,
解:(1)过点A作AF⊥x轴,垂足为点F,过点B作BE⊥x轴,垂足为点E,则AF=
| 3 |
∵OA⊥OB,
∴∠AOF+∠BOE=90°.
又∵∠BOE+∠OBE=90°,
∴∠AOF=∠OBE,
∴Rt△AFO∽Rt△OEB,
∴
| BE |
| OF |
| OE |
| AF |
∴
| ||
| 1 |
| m | ||
|
(2)设过点A(-1,
| 3 |
| 3 |
∴
|
|
∴所求抛物线的表达式为y=
| ||
| 3 |
2
| ||
| 3 |
点评:本题考查了学生待定系数法求解析式,培养了学生数形结合处理问题、解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
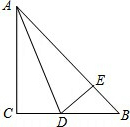 如图所示,在等腰直角△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E.若AB=8,则△DEB的周长为( )
如图所示,在等腰直角△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E.若AB=8,则△DEB的周长为( )| A、6 | B、8 | C、10 | D、12 |
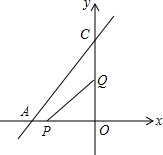 如图,已知直线AC的解析式为y=
如图,已知直线AC的解析式为y= 已知D、B、C是⊙O上三点
已知D、B、C是⊙O上三点
 如图,点A(2,6),y轴上有一点B,使得OB=AB,求点B的坐标.
如图,点A(2,6),y轴上有一点B,使得OB=AB,求点B的坐标. 如图,在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,AD=1,求△ABC的周长与面积.
如图,在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,AD=1,求△ABC的周长与面积. 如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.
如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.