题目内容
数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为|AB|=|a-b|.

根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、-1,
①A、B之间的距离可用含x的式子表示为 ;
②若该两点之间的距离为2,那么x值为 .
(2)|x+1|+|x-2|的最小值为 ,此时x的取值是 ;
(3)已知(|x+1|+|x-2|)(|y-3|+|y+2|)=15,求x-2y的最大值 和最小值 .

根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、-1,
①A、B之间的距离可用含x的式子表示为
②若该两点之间的距离为2,那么x值为
(2)|x+1|+|x-2|的最小值为
(3)已知(|x+1|+|x-2|)(|y-3|+|y+2|)=15,求x-2y的最大值
考点:绝对值,数轴
专题:
分析:(1)①根据题目已知中的A、B两点间的距离表示为|AB|=|a-b|.即可解答;
②使①中的式子等于2,解出即可;
(2)求|x+1|+|x-2|的最小值,由线段的性质,两点之间,线段最短,可知当-1≤x≤2时,|x+1|+|x-2|有最小值,再根据绝对值的性质即可求出最小值及x的取值;
(3)由于(|x+1|+|x-2|)(|y-3|+|y+2|)=15=3×5,可知-1≤x≤2,-2≤y≤3,依此得到x-2y的最大值和最小值.
②使①中的式子等于2,解出即可;
(2)求|x+1|+|x-2|的最小值,由线段的性质,两点之间,线段最短,可知当-1≤x≤2时,|x+1|+|x-2|有最小值,再根据绝对值的性质即可求出最小值及x的取值;
(3)由于(|x+1|+|x-2|)(|y-3|+|y+2|)=15=3×5,可知-1≤x≤2,-2≤y≤3,依此得到x-2y的最大值和最小值.
解答:解:(1)①A、B之间的距离可用含x的式子表示为|x+1|;
②依题意有
|x+1|=2,
x+1=-2或x+1=2,
解得x=-3或x=1.
故x值为-3或1.
(2)|x+1|+|x-2|的最小值为3,此时x的取值是-1≤x≤2;
(3)∵(|x+1|+|x-2|)(|y-3|+|y+2|)=15,
∴-1≤x≤2,-2≤y≤3,
∴x-2y的最大值为2-2×(-2)=6,最小值为-1-2×3=-7.
故x-2y的最大值6,最小值-7.
故答案为:|x+1|;-3或1;3,-1≤x≤2;6,-7.
②依题意有
|x+1|=2,
x+1=-2或x+1=2,
解得x=-3或x=1.
故x值为-3或1.
(2)|x+1|+|x-2|的最小值为3,此时x的取值是-1≤x≤2;
(3)∵(|x+1|+|x-2|)(|y-3|+|y+2|)=15,
∴-1≤x≤2,-2≤y≤3,
∴x-2y的最大值为2-2×(-2)=6,最小值为-1-2×3=-7.
故x-2y的最大值6,最小值-7.
故答案为:|x+1|;-3或1;3,-1≤x≤2;6,-7.
点评:考查了绝对值和数轴,借助数轴可以使有关绝对值的问题转化为数轴上有关距离的问题,反之,有关数轴上的距离问题也可以转化为绝对值问题.这种相互转化在解决某些问题时可以带来方便.事实上,|A-B|表示的几何意义就是在数轴上表示数A与数B的点之间的距离.这是一个很有用的结论,我们正是利用这一结论并结合数轴的知识解决了(2)(3)这两道难题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
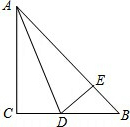 如图所示,在等腰直角△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E.若AB=8,则△DEB的周长为( )
如图所示,在等腰直角△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E.若AB=8,则△DEB的周长为( )| A、6 | B、8 | C、10 | D、12 |
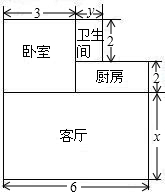 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题: 如图,点A(2,6),y轴上有一点B,使得OB=AB,求点B的坐标.
如图,点A(2,6),y轴上有一点B,使得OB=AB,求点B的坐标.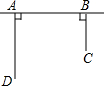 如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等.
如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等. 如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.
如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.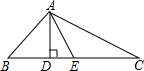 如图,△ABC中,AB=2,BC=5,AC=4.AD、AE分别为CB边上的高和中线,求DE的长.
如图,△ABC中,AB=2,BC=5,AC=4.AD、AE分别为CB边上的高和中线,求DE的长. 如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.
如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.