题目内容
2.下列说法:①带根号的数是无理数;②不含根号的数一定是有理数;③无理数是开方开不尽的数;④无限不循环小数是无理数;⑤π是无理数,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据史书的定义求解即可.
解答 解:①无限不循环小数是无理数故①不符合题意;
②π是无理数,故②不符合题意;
③无限不循环小数是无理数故③不符合题意;
④无限不循环小数是无理数,故④符合题意;
⑤π是无理数,故⑤符合题意,
故选:C.
点评 本题考查了实数,无理数是无限不循环小数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列运算中,正确的是( )
| A. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | B. | $\sqrt{\frac{3}{2}}$=$\frac{\sqrt{3}}{2}$ | C. | $\sqrt{12}$=2$\sqrt{3}$ | D. | $\sqrt{(2-\sqrt{5})^{2}}$=2-$\sqrt{5}$ |
17.在?ABCD中,如果∠A+∠C=160°,那么∠B等于( )
| A. | 20° | B. | 100° | C. | 60° | D. | 80° |
11. 如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
 如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )| A. | AB∥DC,AD∥BC | B. | AB∥DC,AD=BC | C. | AO=CO,BO=DO | D. | AB=DC,AD=BC |
9.下列运算正确的是( )
| A. | $\sqrt{{{({-2})}^2}}=-2$ | B. | $\sqrt{x^2}=x$ | C. | $\sqrt{2}+\sqrt{5}=\sqrt{7}$ | D. | $\sqrt{8}=2\sqrt{2}$ |
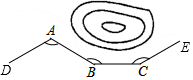 如图所示,一条公路修到湖边时,需要拐弯绕湖而过,第一次拐的角∠A=120°,第二次拐的角∠B=165°,则第三次拐的角∠C=135°时道路CE才能恰好与AD平行.
如图所示,一条公路修到湖边时,需要拐弯绕湖而过,第一次拐的角∠A=120°,第二次拐的角∠B=165°,则第三次拐的角∠C=135°时道路CE才能恰好与AD平行.