题目内容
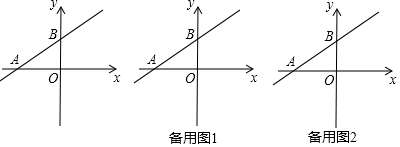
10.如图,在平面直角坐标系中,直线y=kx+3分别交y轴、x轴于B、A两点,且△ABO的面积为$\frac{9\sqrt{3}}{2}$.(1)求直线AB的解析式;
(2)点P从点A出发沿x轴正方向运动,速度为$\sqrt{3}$个单位长度/秒,连接PB,设d=PB2,点P的运动时间为t秒,求d与t的函数关系式,并写出t的取值范围;
(3)在(2)的条件下,过点P作PQ⊥AB交射线AB于点Q,连接PQ,当t为何值时,使△APQ≌△ABO,并求出此时的d的值.
分析 (1)根据题意求出点A的坐标,利用待定系数法即可解决问题;
(2)分两种情形利用勾股定理计算即可解决问题;
(3)由△APQ≌△ABO可知AP=AB,列出方程求出t,即可解决问题;
解答 (1)解:由AB:y=kx+3可得B(0,3)
又因△ABO的面积=$\frac{9\sqrt{3}}{2}$,
∴$\frac{1}{2}$•AO•BO=$\frac{9\sqrt{3}}{2}$,
∴$\frac{1}{2}$•OA•3=$\frac{9\sqrt{3}}{2}$,
AO=3$\sqrt{3}$,
∵点A在x轴的负半轴,
∴A(-3$\sqrt{3}$,0)
将A(-3$\sqrt{3}$,0)代入y=kx+3解得:k=$\frac{\sqrt{3}}{3}$,
∴直线AB的解析式为:y=$\frac{\sqrt{3}}{3}$x+3.
(2)由题意可列:第一种情况:OP=OA-AP=3$\sqrt{3}$-$\sqrt{3}$t
∵d=PB2=AO2+BO2=(3$\sqrt{3}$-$\sqrt{3}$t)2+32=3t2-18t+36(0<t≤3).
第二种情况:OP=AP-OA=$\sqrt{3}$t-3$\sqrt{3}$
∵d=PB2=AO2+BO2=($\sqrt{3}$t-3$\sqrt{3}$)2+32=3t2-18t+36(t>3).
综上所述:d与t的函数关系式是:d=3t2-18t+36(t>0).
(3)∵∠BAO=∠PAO
∠AOB=∠AQP=90°
∴当AP=AB时△APQ≌△ABO,
∵AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=6,
∴,$\sqrt{3}$t=6,解得:t=2$\sqrt{3}$,
∴此时d=3t2-18t+36=3×(2$\sqrt{3}$)2-18×2$\sqrt{3}$+36=72-36$\sqrt{3}$.
点评 本题考查一次函数综合题,待定系数法,勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | -2 | B. | 2 | C. | 3 | D. | 0 |
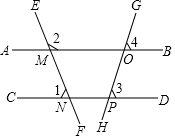 如图,已知∠1=68°,∠3=∠4,求∠2的度数.
如图,已知∠1=68°,∠3=∠4,求∠2的度数.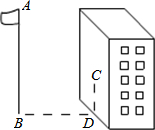 如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.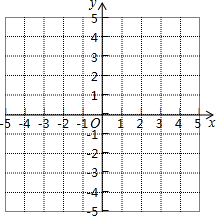 一次函数y=kx+b(k≠0)的图象经过点(-1,-4)和(2,2)
一次函数y=kx+b(k≠0)的图象经过点(-1,-4)和(2,2)