题目内容
7．
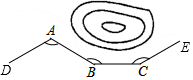如图所示，一条公路修到湖边时，需要拐弯绕湖而过，第一次拐的角∠A=120°，第二次拐的角∠B=165°，则第三次拐的角∠C=135°时道路CE才能恰好与AD平行．
分析 先延长AB，EC，交于点F，根据平行线的性质得出∠F的度数，再根据三角形外角性质进行计算，即可得到∠BCE的度数．
解答 
解：如图，延长AB，EC，交于点F，
当AD∥EF时，∠F=∠A=120°，
∵∠FBC=180°-∠ABC=15°，
∴∠BCE=∠F+∠FBC=120°+15°=135°，
即第三次拐的角为135°时，道路CE才能恰好与AD平行．
故答案为：135．
点评 此题主要考查了平行线性质以及三角形外角性质的运用，关键是掌握两直线平行，内错角相等．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
20．在$\sqrt{\frac{49}{100}}$，$\frac{1}{π}$，$\sqrt{7}$，$\frac{101}{11}$，0.10111213…中，无理数的个数是（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
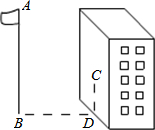如图，某同学相测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的影高为2米，求旗杆的高度．
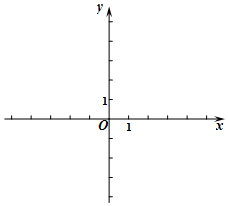已知一次函数y=kx+b的图象经过点A（2，0），与y轴交于点B（0，4）．
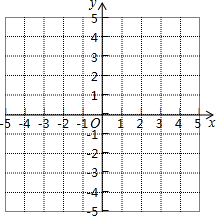一次函数y=kx+b（k≠0）的图象经过点（-1，-4）和（2，2）
16．
如图，能表示点B到直线AC的距离的线段是（ ）
如图，能表示点B到直线AC的距离的线段是（ ）| A． | BC | B． | BD | C． | BA | D． | AD |