Question

2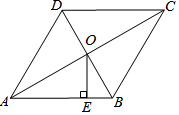．如图，菱形ABCD的对角线AC，BD相交于点O，且AC=16，BD=12．
（1）求菱形ABCD的周长；
（2）过点O作OE⊥AB于点E，求sin∠BOE的值．

Answer 1

分析 （1）由已知条件可求出菱形的边长，进而可求出其周长；
（2）由△AOB的面积为菱形面积的四分之一，可求出OE的长，进而可求出sin∠BOE的值．

解答 解：
（1）∵四边形ABCD是菱形，AC=16，BD=12，
∴AC⊥BD，AO=OC=$\frac{1}{2}$AC=8，BO=BD=$\frac{1}{2}$BD=6，
在Rt△AOB中，由勾股定理得：AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=10，
∴菱形ABCD的周长=4AB=40；
（2）∵菱形ABCD的面积=$\frac{1}{2}$AC•BD=96，
∴△AOB的面积=$\frac{1}{4}$×96=24，
∴OE=$\frac{8×6}{10}$=4.8，
∴BE=3.6，
∴sin∠BOE=$\frac{BE}{OB}$=$\frac{3}{5}$．

点评 本题考查了菱形的性质和勾股定理的应用，熟记菱形的对角线互相垂直平分和菱形ABCD的面积=$\frac{1}{2}$×AC×BD是解题关键．