题目内容
19.(1)化简:($\sqrt{12}$+$\sqrt{3})$×$\sqrt{6}$-2$\sqrt{\frac{1}{2}}$(2)在实数范围内分解因式:2x4-8.
分析 (1)先进行二次根式的乘法运算,然后把二次根式化为最简二次根式后合并即可;
(2)先提2,然后利用平方差公式分解因式.
解答 解:(1)原式=$\sqrt{12×6}$+$\sqrt{3×6}$-$\sqrt{2}$
=6$\sqrt{2}$+3$\sqrt{2}$-$\sqrt{2}$
=$8\sqrt{2}$;
(2)原式=2(x4-4)
=2(x2+2)(x2-2)
=$2({x^2}+2)(x+\sqrt{2})(x-\sqrt{2})$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了因式分解.

练习册系列答案
相关题目
15.如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(6)个图形由( )个正方体叠成.


| A. | 36 | B. | 37 | C. | 56 | D. | 84 |
10. 下列四个图形中是图中的侧面展开图的是( )
下列四个图形中是图中的侧面展开图的是( )
 下列四个图形中是图中的侧面展开图的是( )
下列四个图形中是图中的侧面展开图的是( )| A. |  | B. |  | C. |  | D. |  |
7.已知a,b满足3a=2013,671b=2013,则$\frac{ab}{a+b}$=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
14.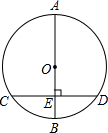 如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
 如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )| A. | 10cm | B. | 14cm | C. | 15cm | D. | 16cm |
4.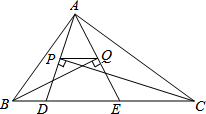 如图,△ABC的周长为30,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
如图,△ABC的周长为30,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
 如图,△ABC的周长为30,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
如图,△ABC的周长为30,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )| A. | $\frac{3}{2}$ | B. | 5 | C. | 3 | D. | 4 |
11.一组数据的最大值为105,最小值为23,若确定组距为9,则分成的组数为( )
| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
8.已知10x=20,5x=8,则2x的值是( )
| A. | $\frac{2}{5}$ | B. | $\frac{5}{2}$ | C. | 12 | D. | 160 |
9. 如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是( )
如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是( )
 如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是( )
如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是( )| A. | 5 m | B. | 15 m | C. | 25 m | D. | 30 m |