题目内容
15.如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(6)个图形由( )个正方体叠成.
| A. | 36 | B. | 37 | C. | 56 | D. | 84 |
分析 根据图形的变换规律,可知第n个图形中的正方体的个数为1+3+6+…+$\frac{n(n+1)}{2}$,据此可得第(6)个图形中正方体的个数.
解答 解:由图可得:
第(1)个图形中正方体的个数为1;
第(2)个图形中正方体的个数为4=1+3;
第(3)个图形中正方体的个数为10=1+3+6;
第(4)个图形中正方体的个数为20=1+3+6+10;
故第n个图形中的正方体的个数为1+3+6+…+$\frac{n(n+1)}{2}$,
∴第(5)个图形中正方体的个数为1+3+6+10+15=35;
第(6)个图形中正方体的个数为1+3+6+10+15+21=56;
故选:C.
点评 本题主要考查了图形变化类问题以及正方体,解决问题的关键是依据图形得到变换规律.解题时注意:第n个图形中的正方体的个数为1+3+6+…+$\frac{n(n+1)}{2}$.

练习册系列答案
相关题目
6.车轮滚动一周,求所行的路程,就是求车轮的( )
| A. | 直径 | B. | 周长 | C. | 面积 | D. | 半径 |
3.单项式-$\frac{2}{5}$a2b3的系数和次数分别是( )
| A. | -$\frac{2}{5}$,2 | B. | $\frac{2}{5}$,3 | C. | -$\frac{2}{5}$,5 | D. | $\frac{2}{5}$,6 |
7.在?ABCD中,AB=3cm,BC=6cm,一组对边之间的距离为4cm,则另一组对边之间的距离为( )
| A. | 8cm | B. | 8cm或2cm | C. | 2cm | D. | 无法确定 |
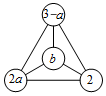 如图,在一个三角形三个顶点和中心处的每个“○”中各填有一个式子,如果图中任意三个“○”中的式子之和均相等,那么a的值为( )
如图,在一个三角形三个顶点和中心处的每个“○”中各填有一个式子,如果图中任意三个“○”中的式子之和均相等,那么a的值为( )