题目内容
7.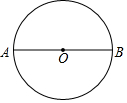 如图,AB是⊙O的直径,AB=2.
如图,AB是⊙O的直径,AB=2.(1)尺规作图(保留作图痕迹,不写作法):作⊙O的内接正六边形ACDBEF.
(2)在(1)的条件下,直线PE与⊙O相切于点E,交AB延长线于点P,求PB、PE和$\widehat{BE}$所围成的图形面积.
分析 (1)直接利用正六边形的性质利用圆的半径分别作弧得出答案;
(2)首先求出S扇形EOB=$\frac{1}{6}$π,进而得出SRt△OEP=$\frac{\sqrt{3}}{2}$,求出PB、PE和$\widehat{BE}$所围成的图形面积即可.
解答 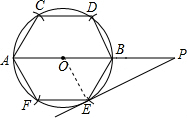 解:(1)如图所示:正六边形ACDBEF即为所求;
解:(1)如图所示:正六边形ACDBEF即为所求;
(2)连结OE,
∵PE切⊙O于E,
∴∠OEP=90°,
∵正六边形ACDBEF内接于⊙O,
∴∠EOB=60°,
∴S扇形EOB=$\frac{1}{6}$π,
∵∠EOB=60°,∠OEP=90°,
∴tan60°=$\frac{EP}{EO}$=$\sqrt{3}$,
∵EO=1,
∴EP=$\sqrt{3}$,
∴SRt△OEP=$\frac{\sqrt{3}}{2}$,
∴S=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
点评 此题主要考查了复杂作图以及扇形面积求法,正确掌握切线的性质是解题关键.

练习册系列答案
相关题目
15.学校最近新配备了一批图书需要甲乙两人进行整理,若甲单独整理完成需要4小时完工;若甲乙共同整理2小时后,乙再单独整理2小时才能完工,则乙单独整理完成需要( )
| A. | 4小时 | B. | 6小时 | C. | 8小时 | D. | 10小时 |
12.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
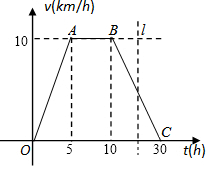 据环保中心观察和预测:发生于甲地的河流污染一直向下游方向移动,其移动速度v(千米/小时)与时间t(小时)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(小时)内污染所经过的路程S(千米).
据环保中心观察和预测:发生于甲地的河流污染一直向下游方向移动,其移动速度v(千米/小时)与时间t(小时)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(小时)内污染所经过的路程S(千米). 如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为90°.
如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为90°.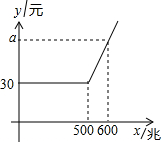 如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )
如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )