题目内容
9.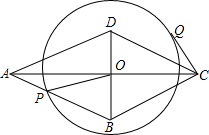 如图:已知菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作⊙O,CQ切⊙O于点Q.则在点P运动过程中,切线CQ的长的最大值为$\frac{16}{5}$.
如图:已知菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作⊙O,CQ切⊙O于点Q.则在点P运动过程中,切线CQ的长的最大值为$\frac{16}{5}$.
分析 首先连接OQ,由CQ切⊙O于点Q,可得当OQ最小时,CQ最大,即当OP⊥AB时,CQ最大,然后由菱形与直角三角形的性质,求得OP的长,继而求得答案.
解答 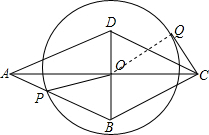 解:连接OQ,
解:连接OQ,
∵CQ切⊙O于点Q,
∴OQ⊥CQ,
∴∠CQO=90°,
∴CQ=$\sqrt{O{C}^{2}-O{Q}^{2}}$,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4,OB=$\frac{1}{2}$BD=$\frac{1}{2}$×6=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∴OC是定值,则当OQ最小时,CQ最大,
即OP最小时,CQ最大,
∴当OP⊥AB时,CQ最大,此时OQ=OP=$\frac{OA•OB}{AB}$=$\frac{12}{5}$,
∴CQ=$\frac{16}{5}$.
故答案为:$\frac{16}{5}$.
点评 此题属于圆的综合题.考查了切线的性质、菱形的性质、直角三角形的性质以及勾股定理等知识.注意得到当OP⊥AB时,CQ最大是关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
4.下列几组数中,是勾股数的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 15,8,17 | C. | 13,14,15 | D. | $\frac{3}{5}$,$\frac{4}{5}$,1 |
14.据报道,截至2015年12月底,我区户籍人口突破90万,是沈阳户籍人口最多的区,数据“90万”用科学记数法可表示为( )
| A. | 90×104 | B. | 9×104 | C. | 9×105 | D. | 0.9×105 |
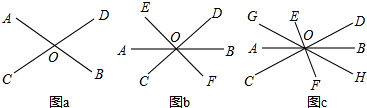
3. 如图,下列条件中,能判断AB∥CD的是( )
如图,下列条件中,能判断AB∥CD的是( )
 如图,下列条件中,能判断AB∥CD的是( )
如图,下列条件中,能判断AB∥CD的是( )| A. | ∠1=∠3 | B. | ∠2=∠3 | C. | ∠4=∠5 | D. | ∠3+∠4=180° |
4.下列说法中正确的是( )
| A. | 对顶角相等 | B. | 有一条公共边的两个角互补 | ||
| C. | 相等的两个角是对顶角 | D. | 互补的两个角是邻补角 |
 如图,正方体的棱长为5,一只蚂蚁如果要沿着正方体的表面从点A爬到点B,需要爬行的最短距离是5$\sqrt{5}$.
如图,正方体的棱长为5,一只蚂蚁如果要沿着正方体的表面从点A爬到点B,需要爬行的最短距离是5$\sqrt{5}$.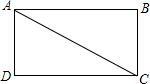 如图,矩形ABCD的两邻边长分别为一元二次方程x2-7x+12=0的两个实数根,则矩形ABCD的面积为12.
如图,矩形ABCD的两邻边长分别为一元二次方程x2-7x+12=0的两个实数根,则矩形ABCD的面积为12.