题目内容
13.已知一次函数的图象经过A(0,-3)、B(1,a)、C(a,1)三点,图象与x轴交于点D,且函数值y随着x的值增大而增大,点P在直线AB上;(1)求这个一次函数的解析式,并画出函数图象;
(2)当P(x,y)是第一象限内直线上的点时,若用点P的横坐标x表示S△POD,则S与x有怎样的函数关系式?并写出x的取值范围;
(3)写出S等于1时,x的值.
分析 (1)设一次函数解析式为y=kx+b,把A坐标代入求出b的值,把B与C坐标代入求出k的值,即可确定出解析式;
(2)对于一次函数解析式,令y=0求出x的值,确定出D坐标,进而表示出OD的长,P纵坐标为OD边上的高,利用三角形面积公式表示出S与x的关系式即可;
(3)令S=1,求出x的值即可.
解答 解:(1)设一次函数解析式为y=kx+b,
把A(0,-3)代入得:b=-3,
把B与C坐标代入得:$\left\{\begin{array}{l}{k-3=a}\\{ak-3=1}\end{array}\right.$,
解得:k=4或k=-1,
∵函数值y随着x的值增大而增大,
∴k=4,
则一次函数解析式为y=4x-3;
函数图象如图: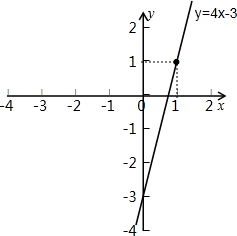
(2)对于一次函数y=4x-3,令y=0,得到x=$\frac{3}{4}$,即D($\frac{3}{4}$,0),
则S△POD=$\frac{1}{2}$×$\frac{3}{4}$(4x-3)=$\frac{3}{2}$x-$\frac{9}{8}$(x>0);
(3)令S=1,得到$\frac{3}{2}$x-$\frac{9}{8}$=1,
解得:x=$\frac{17}{12}$.
点评 此题考查了待定系数法求一次函数解析式,以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.如果1-x是负数,那么x的取值范围是( )
| A. | x>0 | B. | x<0 | C. | x>1 | D. | x<1 |
3.初三(8)班体委用划记法统计本班40名同学投掷实心球的成绩,结果如下表所示:
则这40名同学投掷实心球的成绩的众数和中位数分别是( )
| 成绩(分) | 6 | 7 | 8 | 9 | 10 |
| 人数 |  | 正 一 | 正 正 一 | 正 正  | 正 |
| A. | 9,8 | B. | 9,8.5 | C. | 8,8 | D. | 8,8.5 |
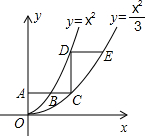 如图,平行于x轴的直线AC分别交抛物线${y_1}={x^2}$(x≥0)与${y_2}=\frac{x^2}{3}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E.若已知点A的纵坐标为1,则CD的长度为2,$\frac{DE}{AB}$=3-$\sqrt{3}$.
如图,平行于x轴的直线AC分别交抛物线${y_1}={x^2}$(x≥0)与${y_2}=\frac{x^2}{3}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E.若已知点A的纵坐标为1,则CD的长度为2,$\frac{DE}{AB}$=3-$\sqrt{3}$.