题目内容
计算或化解求值
(1)先化简,再求值:
÷(
-4),其中x=
.
(2)已知x2-2x-7=0,求(x-2)2+(x+3)(x-3)的值.
(1)先化简,再求值:
| x2-4 |
| x2+2x |
| x2+4 |
| x |
| 5 |
(2)已知x2-2x-7=0,求(x-2)2+(x+3)(x-3)的值.
考点:分式的化简求值,整式的混合运算—化简求值
专题:计算题
分析:(1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值;
(2)原式利用完全平方公式及平方差公式化简,去括号合并得到最简结果,把已知等式变形后代入计算即可求出值.
(2)原式利用完全平方公式及平方差公式化简,去括号合并得到最简结果,把已知等式变形后代入计算即可求出值.
解答:解:(1)原式=
÷
=
•
=
,
当x=
时,原式=
=
+2;
(2)原式=x2-4x+4+x2-9=2x2-4x-5=2(x2-2x)-5,
∵x2-2x-7=0,∴x2-2x=7,
则原式=14-5=9.
| (x+2)(x-2) |
| x(x+2) |
| x2+4-4x |
| x |
| x-2 |
| x |
| x |
| (x-2)2 |
| 1 |
| x-2 |
当x=
| 5 |
| 1 | ||
|
| 5 |
(2)原式=x2-4x+4+x2-9=2x2-4x-5=2(x2-2x)-5,
∵x2-2x-7=0,∴x2-2x=7,
则原式=14-5=9.
点评:此题考查了分式的化简求值,以及整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
关于x的方程(x+m)2=n能用直接开平方法解的条件是( )
| A、m≥0,n≥0 |
| B、m≥0,n≤0 |
| C、m为任意数,n≥0 |
| D、m为任意数,n>0 |
 如图,要在一块长30m,宽20m的长方形草地四周,设计一条等宽的小路,如果要使小路所占的面积是原长方形草地面积的六分之一,应如何设计小路的宽度?(结果保留根号).
如图,要在一块长30m,宽20m的长方形草地四周,设计一条等宽的小路,如果要使小路所占的面积是原长方形草地面积的六分之一,应如何设计小路的宽度?(结果保留根号).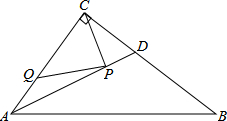 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )